An object is placed 12cm to the left of a converging lens of focal length 8cm. another converging lens of 6cm focal length is placed at a distance of 30cm to the right of the first lens. The second lens will produceSolution in Kannada
a virtual enlarged image
no image
a real inverted image
a real enlarged image.
The correct Answer is:C
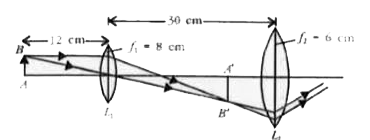
AB is the object and A.B. is the image formed by the first lens L1.
Image distance (v) is calculated from the relation,
1v−1u=1f (Lens formula)
Here, u=+12cm, f=-8cm.
[Distance measured along the direction of the incident ray is taken as negative].
∴1v−112=−18⇒v=−24cm.
So the first lens L1 will form a real image at a distance of 24 cm to the right of it. this image will act as the object for the second lens L2.
Now, the object distance for the second lens
L2=30−24=6cm.
Since the focal length of the 2nd lens is 6cm, the object is now placed at the focus of the 2nd lens. hence the image will be formed at infinity which will be real and inverted.
Topper's Solved these Questions
Similar Questions
A balloon starts rising from thee ground with an acceleration of 1.25m/s2. After 8 s, a stone is released from the balloon. The stone will (taking g=10ms−2)
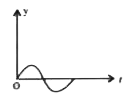
View SolutionThe displacement time graph of a particle executing SHM is as shown in the figure. The corresponding force-time graph of the particle is-
View SolutionAn object is placed 12 cm to the left of a diverging lens of focal length -6.0 cm. A converging lens with a focal length of 12.0 cm is placed at a distance d to the right of the diverging lens. Find the distance d that corresponds to a final image at infinity.
View SolutionWhen an object is placed at the proper distance ot the left of a converging lens, the image is focused in a screen 30 cm to the right of lens. A dieverging lens is now placed 15 cm to the right of the converging lens and it is found that the screen must be moved 19.2cm farther to the right to obtain a sharp image. Find the focal length of the diverging lens.
View SolutionAn object is placed 12 cm to the left of a converging lens of focal length 8cm . Another converging lens of 6 cm focal lengh is placed at a distance of 30 cm to the right of the first lens. The second lens will produce
View SolutionAn illuminated object is placed at a distance of 20 cm from a converging lens of focal length 15 cm. The image obtained on the screen is:
View SolutionSome rays falling on a converging lens are focussed 20 cm from the lens. When a diverging lens is placed in contact with the converging lens, the rays are focussed 30 cm from the combination. What is the focal length of the diverging lens?
View SolutionThe focal length of convex lens is 20 cm. If an object of height 4 cm is placed at a distance of 30 cm from the lens, find:
The magnification produced by the lens.
View SolutionAn object is placed at 50 cm from a lens produces a virtual image at a distance of 10 cm in front of the lens . What is the focal length of the lens ? Is it converging or diverging ?
View SolutionA converging lens of focal length 30 cm is placed in contact with another converging lens of unknown focal length, then possible value for focal length of combination is
View Solutionएक वस्तु को 8 सेमी फोकस दूरी वाले अभिसारी लेन्स के बाँयी ओर 12 सेमी दूर रखा है । 6 सेमी दूरी वाला अन्य अभिसारी लेन्स पहले लेन्स के दाँयी ओर 30 सेमी दूर रखा है । दूसरा लेन्स बनायेगा
View SolutionA converging lens of focal length 5.0 cm is is placed in contact with a diverging lens of focal length 10.0 cm find the combined focal length of the system .
View SolutionAn object is placed 12 cm to the left of a diverging lens of focal length -6.0 cm. A converging lens of focal length of 12.0 cm is placed at a distance d to the right of the diverging lens. Find the distance d that corresponds to a final image at infinity.
View SolutionWhat is the focal length of a convex lens of focal length 30 cm in contact with a concave lens of focal length 20cm? Is the system a converging or a diverging lens?
View SolutionThe focal length of convex lens is 20 cm. If an object of height 4 cm is placed at a distance of 30 cm from the lens, find: The magnification produced by the lens.
View Solution

