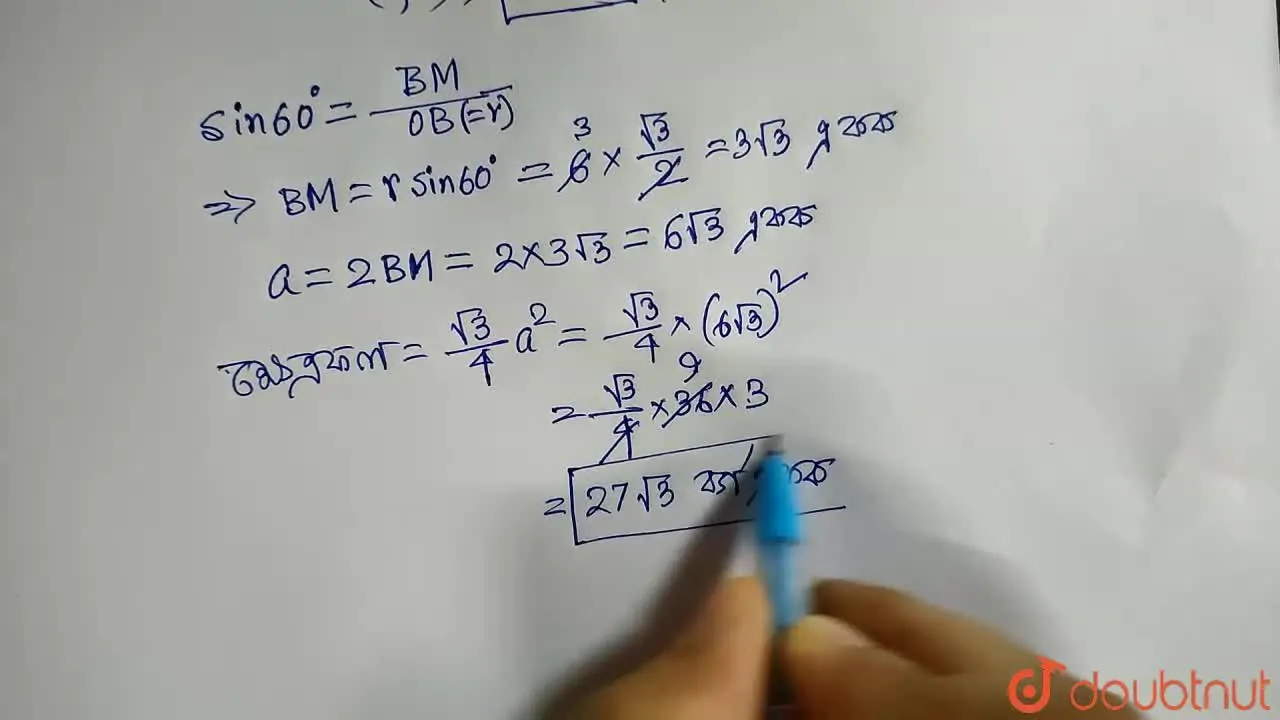যে সমবাহু ত্রিভুজের শীর্ষবিন্দুগুলি x2+y2−4x−6y−23=0 বৃত্তের পরিধির ওপর অবস্থিত তার ক্ষেত্রফল (বর্গ এককে) হবে-
27√2
27√3
27√5
25√3
The correct Answer is:B
B
Related Playlists
Similar Questions
কোনাে একটি পরিসংখ্যা বিভাজনে মধ্য থেকে নির্ণিত গড় পার্থক্যটি—
03:39View Solutionsin(A+B)sin(A−B)=
05:28View SolutionThe circles x2+y2−4x−6y−12=0 and x2+y2+4x+6y+4=0
05:07View SolutionThe area (in sq. units) of an equilateral triangle inscribed in the circle x2+y2−4x−6y−23=0 is -
03:16View Solutionउस वृत्त के केन्द्र का बिन्दुपथ जो वृत्तों
x2+y2+4x−6y+9=0
तथा x2+y2−4x+6y+4=0
को लम्बवत् प्रतिच्छेदित करता है, हैView Solutionवृत्त x2+y2−4x−6y−23=0 का केन्द्र व त्रिज्या ज्ञात करें।
03:24View Solutionযে ত্রিভুজের শীর্ষ বিন্দু তিনটি o,z এবং z(cosalpha+isinalpha)(0ltalphaltpi) জটিল রাশির দ্বারা সূচিত হয় তার ক্ষেত্রফল হবে-
05:53View Solution[θ=srঅথবা কণ (বৃত্তীয় মানে )=(চাপ)/(ব্যাসার্ধ),সূত্র−সম্পর্কিতপেশ্নাবলি।]দুটিবৃত্তএমনযে,একটিঅপরটিকেন্দ্রবিন্দুগামী।প্রথমবৃত্তেরlদৈর্ঘ্যেরচাপতারকেন্দ্রেthetaএবংদ্বিতীয়বৃত্তেরmদৈর্ঘ্যেরচাপতারকেন্দ্রেphiসম্মুখকোণউৎপন্নকরে।প্রমাণকরােযে,lphi=mtheta।
03:36View Solutionx+y+1=0সরলরেখাস্থযেবিন্দু3x+4y +2 = 0-এর থেকে 1/5 একক দূরত্বে অবস্থিত সেই বিন্দুর স্থানাঙক হল—
02:17View Solutionমনে করো xy সমতলে অবস্থিত S একটি বৃত্ত, যা x2+y2 = 4 সমীকরণ দ্বারা সংজ্ঞাত। মনে করো S বৃত্তের ওপর P এমন একটি বিন্দু যার স্থানাঙ্ক দুটি (x স্থানাঙ্ক ও yস্থানাঙ্ক) ধনাত্মক। মনে করো P বিন্দুতে S বৃত্তের স্পর্শক অক্ষদ্বয়কে M ও N বিন্দুতে ছেদ করেছে। তবে MN সরলরেখার মধ্যবিন্দু যে বক্রের ওপর অবস্থিত, তা হল—
03:01View SolutionThe point of contact of the circles x2+y2−4x+6y−3=0andx2+y2+16x+6y+37=0 is
04:48View SolutionLocus of the points of intersection of perpendicular tangents drawn one to each of the circles x2+y2−4x+6y−37=0,x2+y2−4x+6y−37=0,x2+y2−4x+6y−20=0 is
04:33View SolutionThe angle between the pair of tangents drawn from a point P to the circle x2+y2+4x−6y+9sin2α+13cos2α=0 is 2α . then the equation of the locus of the point P is a. x2+y2+4x−6y+4=0 b. x2+y2+4x−6y−9=0 c. x2+y2+4x−6y−4=0 d, x2+y2+4x−6y+9=0
03:05View Solutionउस वृत्त के केन्द्र का बिन्दुपथ जो वृत्तों x2+y2+4x−6y+9=0 तथा x2+y2−4x+6y+4=0 को लम्बवत् प्रतिच्छेदित करता है, है
04:42View Solutionसमीकरण x2+y2+4x+6y+13=0 प्रदर्शित करता है
12:11View Solutionउस वृत्त के केन्द्र का बिन्दुपथ जो वृत्तों x2+y2+4x−6y+9=0 तथा x2+y2−4x+6y+4=0 को लम्बवत् प्रतिच्छेदित करता है, है
03:45View Solution