There are 40 presons in a group : four of them can speak neither Englis nor Hindi .The sum of the number of persons who can speak English and that of those who can speak Hindi is 44 Find the number of those who can speak both English and Hindi.
To solve the problem step by step, we can follow these instructions:
Step 1: Understand the total number of people in the group
We are given that there are 40 persons in total in the group.
Step 2: Identify those who can speak neither language
Out of these 40 persons, 4 can speak neither English nor Hindi. Therefore, the number of people who can speak at least one of the languages (English or Hindi) is:
40−4=36
Step 3: Set up the equation for the sum of speakers
We know that the sum of the number of persons who can speak English (let's denote it as E) and the number of persons who can speak Hindi (denote it as H) is 44:
E+H=44
Step 4: Use the principle of inclusion-exclusion
According to the principle of inclusion-exclusion for two sets, we have:
E+H−(E∩H)=36
Where E∩H represents the number of persons who can speak both English and Hindi.
Step 5: Substitute the known values into the equation
Substituting E+H=44 into the inclusion-exclusion equation gives us:
44−(E∩H)=36
Step 6: Solve for the number of persons who can speak both languages
Now, we can rearrange the equation to find E∩H:
E∩H=44−36
E∩H=8
Conclusion
Thus, the number of persons who can speak both English and Hindi is 8.
---
We are given that there are 40 persons in total in the group.
Out of these 40 persons, 4 can speak neither English nor Hindi. Therefore, the number of people who can speak at least one of the languages (English or Hindi) is:
40−4=36
We know that the sum of the number of persons who can speak English (let's denote it as E) and the number of persons who can speak Hindi (denote it as H) is 44:
E+H=44
According to the principle of inclusion-exclusion for two sets, we have:
E+H−(E∩H)=36
Where E∩H represents the number of persons who can speak both English and Hindi.
Substituting E+H=44 into the inclusion-exclusion equation gives us:
44−(E∩H)=36
Now, we can rearrange the equation to find E∩H:
E∩H=44−36
E∩H=8
Thus, the number of persons who can speak both English and Hindi is 8.
Topper's Solved these Questions
- Set theoryBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - Set theoryEXERCISE - Very short Answer type question
28 Videos
- Set theoryBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - Set theoryEXERCISE - Short Answer type question
24 Videos
- RATIO AND ITS APPLICATIONSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - RATIO AND ITS APPLICATIONSEXERCISE - ASSESSMENT TESTS (TEST 2)
12 Videos
- SIMPLE INTEREST AND COMPOUND INTEREST BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - SIMPLE INTEREST AND COMPOUND INTEREST EXERCISE - Level 3
9 Videos
Similar Questions
There are 40 presons in a group : four of them can speak neither Englis nor Hindi .The sum of the number of persons who can speak English and that of those who can speak Hindi is 44 Find the number of those who can speak both English and Hindi.
View SolutionEach person in a group of 80 can speak either Hindi or English or both. If 55 persons can speak English and 40 can speak both, find the number of persons who can speak Hindi.
View Solution
Knowledge Check
In a group of 850 persons, 600 can speak Hindi and 340 can speak Tamil. Find (i) how many can speak both Hindi and Tamil,
(ii) how many can speak Hindi only,
(iii) how many can speak Tamil only.A60B70C80D90Find out the number of all those people who can speak Tamil and Telugu?
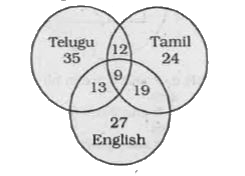 A3B59C21D112
A3B59C21D112In a class of 45 student, 22 can speak hindi and 12 can speck English only ,Find the number of students , who can speak both Hindi and English -
A9B11C23D17
One who can speak two languages.
View SolutionYou, he and she can speak English, can't they?
View SolutionIn a group of 25 students, 13 can speak English, 12 can speak Hindi and speak neither. How many can speak
(i) Both English and Hindi ?
(ii) Only Hindi ?
(iii) Exactly one of the two languages ?
View SolutionIn a survey of population of 450 people, it is found that 205 can speak English, 210 can speak Hindi and 120 people can speak Tamil. If 100 people can speak both Hindi and English, 80 people can speak both English and Tamil, 35 people can speak Hindi and Tamil and 20 people can speak all the three languages, find the number of people who can speak English but not a Hindi or Tamil. Find also the number of people who can speak neither English nor Hindi nor Tamil.
View SolutionIn a group of 1000 people, there are 750 people, who can speak Hindi and 400 people, who can speak Bengali.
(i) Find number of people who can speak Hindi only.
(ii) Number of people who can speak Bengali only is
(iii) Number of people who can speak both Hindi and Bengali is
View Solution