Tangents are drawn to the hyperbola $4 x^{2} - y^{2} = 36$ at the points P and Q. If these tangents intersect at the point T(0,3) then the area (in sq units) of $△ P T Q$ is

$45 \sqrt{5}$

$54 \sqrt{3}$

$60 \sqrt{3}$

$36 \sqrt{5}$

Video Solution

Text Solution

Verified by Experts

Tangents are drawn to the hyperbola $4 x^{2} - y^{2} = 36$ at the point P and Q.
Tangent intersects at point $T (0, 3)$

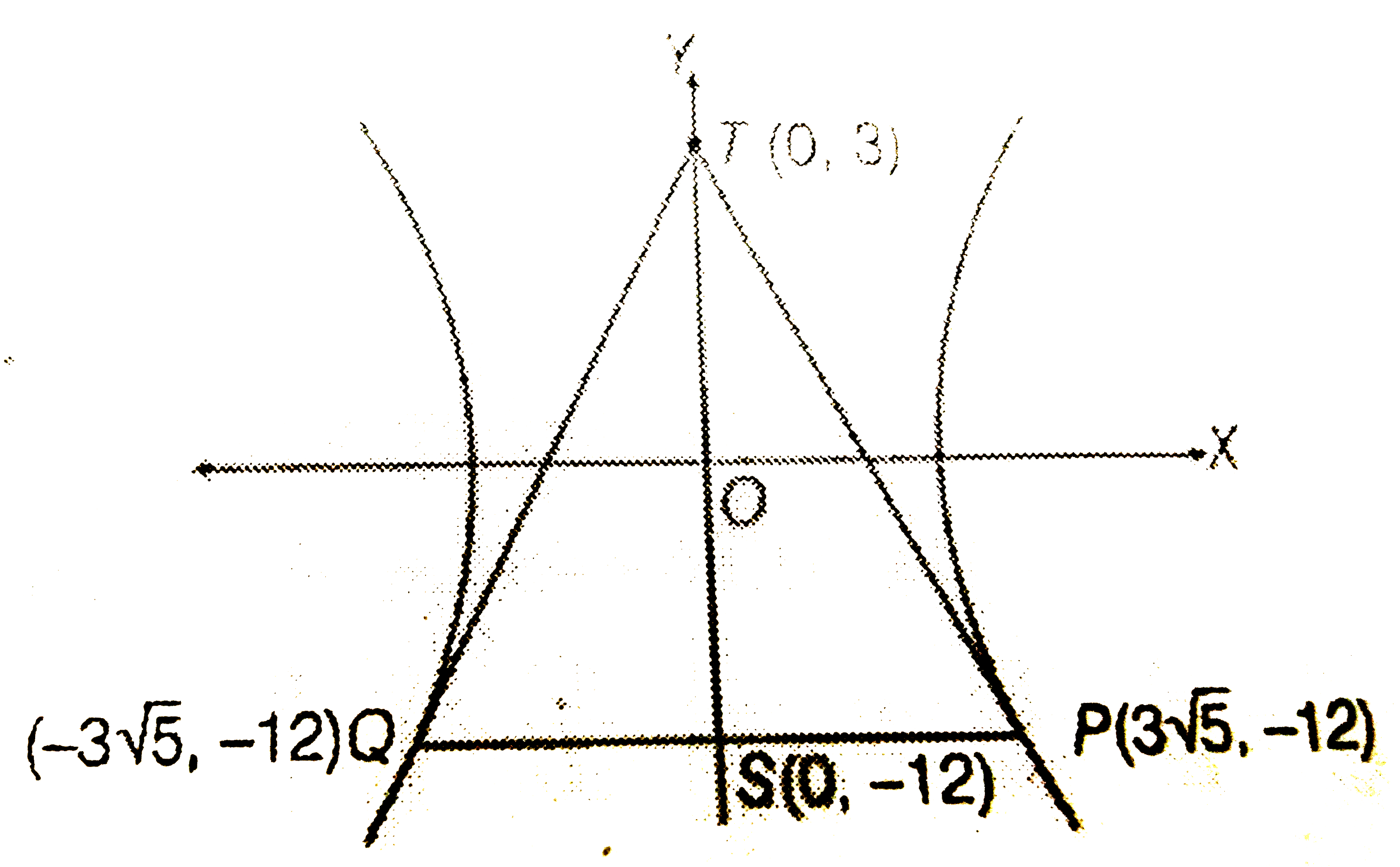
Clearly, PQ is chord of contact.
$∴ Equation of PQ is - 3 y = 36$
$\Rightarrow y = - 12$
Solving the curve $4 x^{2} - y^{2} = 36 and y = - 12$ ,
we get $x = \pm 3 \sqrt{5}$
Area of $△ P Q T = \frac{1}{2} \times P Q \times S T = \frac{1}{2} (6 \sqrt{5} \times 15) = 45 \sqrt{5}$

Updated on:21/07/2023

The tangent and normal to the ellipse $3 x^{2} + 5 y^{2} = 32$ at the point P(2, 2) meet the x-axis at Q and R, respectively. Then the area (in sq. units) of the triangle PQR is:
A $\frac{34}{15}$
B $\frac{16}{3}$
C $\frac{68}{15}$
D $\frac{14}{3}$
Tangents are drawn to the circle $x^{2} + y^{2} = 16$ at the points where it intersects the circle $x^{2} + y^{2} - 6 x - 8 y - 8 = 0$ , then the point of intersection of these tangents is
A $(4, \frac{16}{3})$
B $(12, 16)$
C $(3, 4)$
D $(16, 12)$
Tangents drawn from the point (-8,0) to the parabola $y^{2} = 8 x$ touch the parabola at P and Q. If F is the focus of the parabola, then the area of the triangle PFQ (in sq. units) is equal to:
A24
B64
C32
D48