A variable straight line with slope $m (m \neq 0)$ intersects the hyperbola xy=1 at two distinct points. Then the locus of the point which divides the line segment between these two points in the ratio 1:2 is (A) An ellipse (C) A circle (B) A hyperbola (D) A parabola

Video Solution

Text Solution

Verified by Experts

Let $y = 4 x = c meets x y = 1$ at two points A and B.

i.e. $A (t_{1}, 1 / t_{1}), B (t_{2}, 1 / t_{2})$
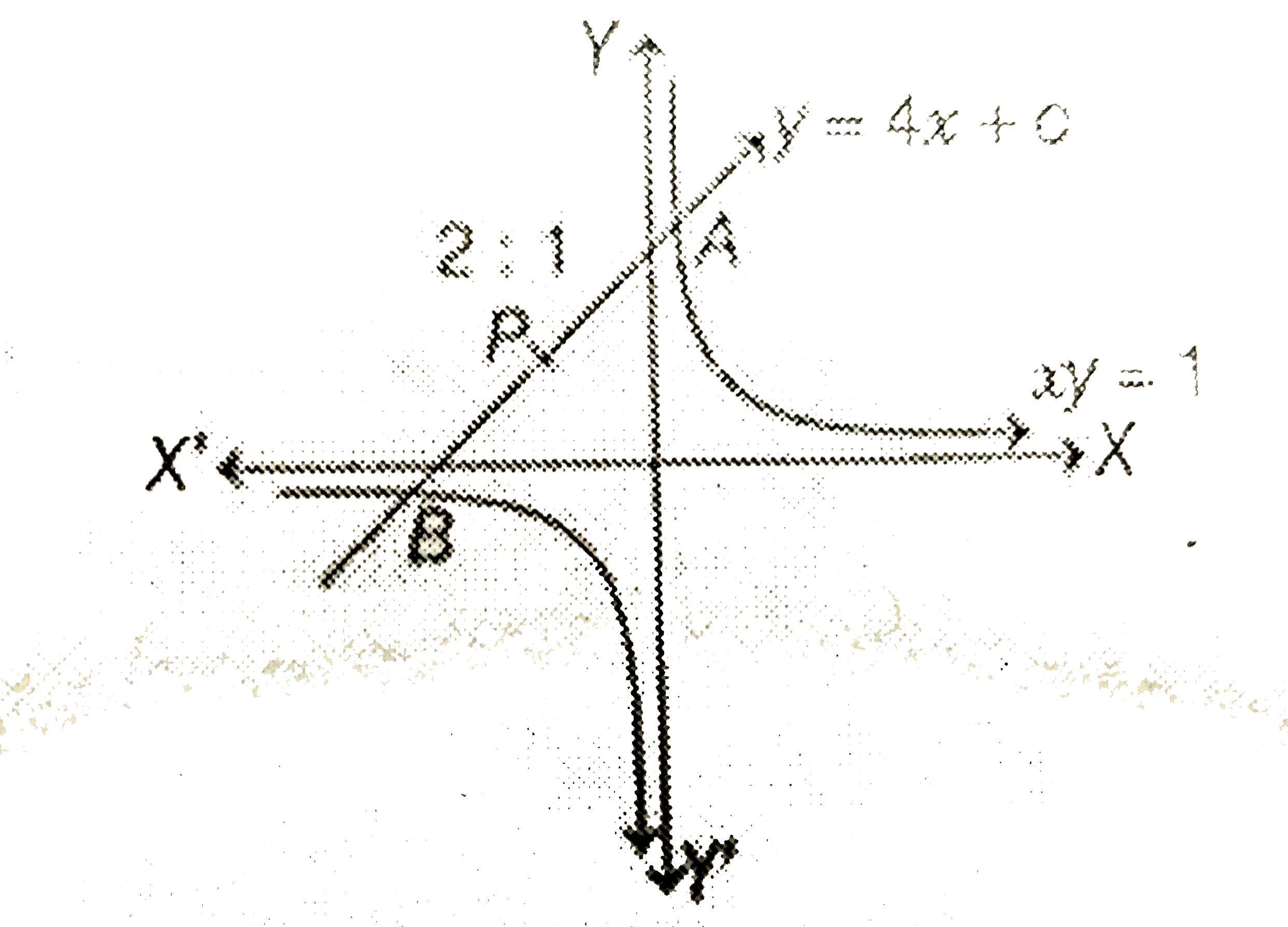
$t h e r e r f or e$ Coordinates of P are
$(\frac{2 t_{1} + t_{2}}{2 + 1}, \frac{2 \cdot \frac{1}{t_{1}} + 1 \cdot \frac{1}{t_{2}}}{2 + 1}) = (h, k) [say]$
$∴ h = \frac{2 t_{1} + t_{2}}{3} and k = \frac{2 t_{2} + t_{1}}{3 t_{1} t_{2}} ...(i)$
Also, $(t_{1}, \frac{1}{t_{1}}) and (t_{2}, \frac{1}{t_{2}}) lie on y = 4 x + c$
$\Rightarrow \frac{\frac{1}{t_{2}} - \frac{1}{t_{1}}}{t_{2} - t_{1}} = \frac{1}{t_{1} t_{2}} = 4 or t_{1} t_{2} = - 1 / 4 ...(ii)$
From Eq. (i), $t_{1} = 2 h + \frac{k}{4}$
$and t_{1} = h - \frac{k}{2} ...(iii)$
From Eqs. (ii) and (iii), $(- h - \frac{k}{2}) (2 h + \frac{k}{4}) = - \frac{1}{4}$
$\Rightarrow - (\frac{2 h + k}{2}) (\frac{8 h + k}{4}) = - \frac{1}{4}$
$\Rightarrow (2 h + k) (8 h + k) = 2$
$\Rightarrow 16 h^{2} + k^{2} + 10 h k = 2$
Hence, required locus is $16 x^{2} + y^{2} + 10 x y = 2 .$

Updated on:21/07/2023

A variable straight line of slope $4$ intersects the hyperbola $x y = 1$ at two points. The locus of the point which divides the line segment between these two points in the ratio $1 : 2$ is
A $16 x^{2} + 10 x y + y^{2} = 2$
B $16 x^{2} - 10 x y + y^{2} = 2$
C $16 x^{2} + 10 x y + y^{2} = 4$
Dnone of these
The straight line $y = m (x - a)$ meets the parabola $y^{2} = 4 a x$ in two distinct points for
Aall $m \in R$
Ball $m \in [- 1, 1]$
Call $m \in R - {0}$
DNone of these
If the extremities of a line segment of length l moves in two fixed perpendicular straight lines, then the locus of the point which divides this line segment in the ratio 1 : 2 is-
Aa parabola
Ban ellipse
Ca hyperbola
DNone of these