A conducting spherical shell of radius R has a charge Q. A small sphere of radius r0(r0<R) currying a charge g is introduced inside the large shell. What is the potential
i. at a point r (r>r0) due to inner sphere
ii. it at a point r=R
iii. at a point r=r0Solution in Tamil
i.V0=14πε0qr
ii. V=14πε0R[Q+e]
iii. V=14πε[qr0+QR]
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NEW JOYTHI PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Previous Year Questions
2 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NEW JOYTHI PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Competitive Exam Corner
22 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NEW JOYTHI PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Practice Problems For Self Assessment
23 Videos
- ELECTROMAGNETIC WAVES BOOK - NEW JOYTHI PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - COMPETITIVE EXAM CORNER
16 Videos
- MAGNETISM AND MATTERBOOK - NEW JOYTHI PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - COMPETITIVE EXAM CORNER
13 Videos
Similar Questions
A. A device to store electrical charge is called
a. Transformer
b. Capacitor
c. Resistor d. Inductor
B. What is meant by energy density of a parallel plate capacitor?
C. Derive an expression for the energy stored in a parallel plate capacitor.
D. What is the area of the plates of a 0.1μF parallel plate air capacitor, given that the separation between the plates is 0.1 mm.
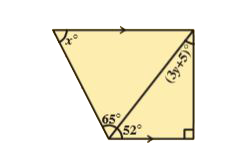
View SolutionFrom the figure find x and y.
View SolutionCalculating the work done in eV in carrying a charge +e Coulomb through a potential rise of 100 volts. (1.0eV=1.6×10−19joules)
View SolutionIf the total electromagnetic energy falling on a surface is U, then the total momentum delivered (for complete absorption) is
View SolutionChoose the correct statement .
View SolutionA point charge q is placed inside a conducting spherical shell of inner radius 2 R and outer radius 3 R at a distance of R from the center of the shell. Find the electric potential at the center of the shell.
View SolutionA thin spherical conducting shell of radius r_(1) carries a charge Q . Concentric with it is another thin metallic spherical shell of radius r_(2) (r_(2) gt r_(1)) . Calculate electric field at distance r when (i) r lt r_(1) ,(ii) r_(1) lt r lt r_(2) and (iii) r gt r_(2) . What will be the field in above cases if outer shell (a) is given charge q and (b) is earthed ?
View SolutionA sphere of radius R contains charge density rho(r )=A (R-r ) , for 0 lt r lt R . The total electric charge inside the sphere is Q. The value of A in terms of Q and R is
View SolutionA sphere of radius R contains charge density rho(r )=A (R-r ) , for 0 lt r lt R . The total electric charge inside the sphere is Q. The electric field inside the sphere is
View SolutionA charge +q is placed somewhere inside the cavity of a thick conducting spherical shell of inner radius R_(1) and outer radius R_(2) . A charge – Q is placed at a distance r gt R_(2) from the centre of the shell. Then the electric field in the hollow cavity-
View SolutionTwo concentric uniformly charge spherical shells of radius R_(1) and R_(2) (R_(2) gt R_(1)) have total charges Q_(1) and Q_(2) respectively. Derive an expression of electric field as a function of r for following positions. (i) r lt R_(1) (ii) R_(1) le r lt R_(2) (iii) r ge R_(2)
View SolutionTwo concentric spherical shells of radius R_(1) and R_(2) (R_(2) gt R_(1)) are having uniformly distributed charges Q_(1) and Q_(2) respectively. Find out potential (i) at point (ii) at surface of smaller shell (i.e. at point B) (iii) at surface of larger shell (i.e. at point C) (iv) at r le R_(1) (v) at R_(1) le r le R_(2) (vi) at r ge R_(2)
View SolutionTwo concentric thin metallic spherical shells of radii R_(1) and R_(2) (where R_(1) lt R_(2) ) are charged with q_(1) and q_(2) coulombs, respectively. Using Gauss' theorem show that, (i) the electric field intensity for radius r lt R_(1) is zero, (ii) the electic field intensity for radius r, where R_(1) lt r lt R_(2), is (1)/(4pi epsilon_(0)).(q_(1))/(r^(2)) and (iii) the electri field intensity for radius r gt R_(2) is (1)/(4pi epsilon_(0)).(q_(1)+q_(2))/(r^(2)) .
View SolutionFor a solid sphere of radius "R" and total charge "Q" let the charge distribution be rho=(Qr)/(pi R^(4)) .Then,for a point P distinct r_(1) from centre of sphere ( r_(1)
View SolutionFor a solid sphere of radius "R" and "total charge "Q" let the charge distribution be ρ=QrπR4.Then,for a point "P" distinct r1 from centre of sphere (r1
View Solution
