A point charge +10μC is at a distance 5 cm directly above the centre of a square of side 10 cm, as shown in figure. What is the magnitude of the electric flux through the square? (Hint: Think of the square as one face of a cube with edge 10cm) 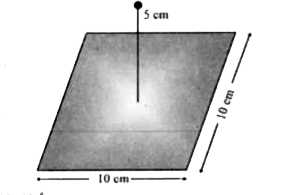 Solution in Tamil
Solution in Tamil
ϕ=1ε0q=1×10×10−68.85×10−12=1.13×106Nm2C−1
Flux through the square =1.13×1066=1.88×105Nm2C−1
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS Book:NEW JOYTHI PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:Evaluation Questions And Answers
Explore 12 Videos
- ELECTRIC CHARGES AND FIELDS Book:NEW JOYTHI PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:Previous Year Questions
Explore 3 Videos
- ELECTRIC CHARGES AND FIELDS Book:NEW JOYTHI PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:Competitive Exam Corner
Explore 20 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:NEW JOYTHI PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:COMPETITIVE EXAM CORNER
Explore 15 Videos
- ELECTROMAGNETIC INDUCTION Book:NEW JOYTHI PUBLICATIONChapter:ELECTROMAGNETIC INDUCTION Exercise:COMPETITIVE EXAM CORNER
Explore 13 Videos
Similar Questions
A glass rod rubbed with silk is brought close to two uncharged spheres in contact with each other inducing charges on them as shown in figure.
a. What happens when the spheres are slightly separated.
b. the glass rod is subsequently removed.
c. the spheres are separated far apart.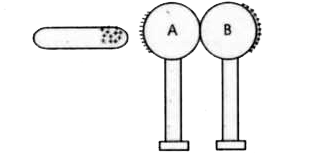
View SolutionMatch column I with II.

View SolutionTwo charged spherical conductors of radii R1andR2 are connected by a wire. Then the ratio of surface charge densitites of the spheres σ1/σ2 is
View SolutionIf 'm' is the mass of an electron and 'c' is the speed of light, the ratio of the wavelength of a photon of energy E to that of the electron of the same energy is
View SolutionA 50 Hz ac current of peak value 2 A flows through one of the pair of coils. If the mutual inductance between the pair of coils is 150 mH, then the peak value of voltage induced in the second coil is
View SolutionA point charge +10μC is at distance of 5cm directly above the center of a square of side 10 cm as shown in Fig. What is the magnitude of the electric flux through the square ? (Hint. Think of the square of the square as one face of a cube with edge 10 cm)
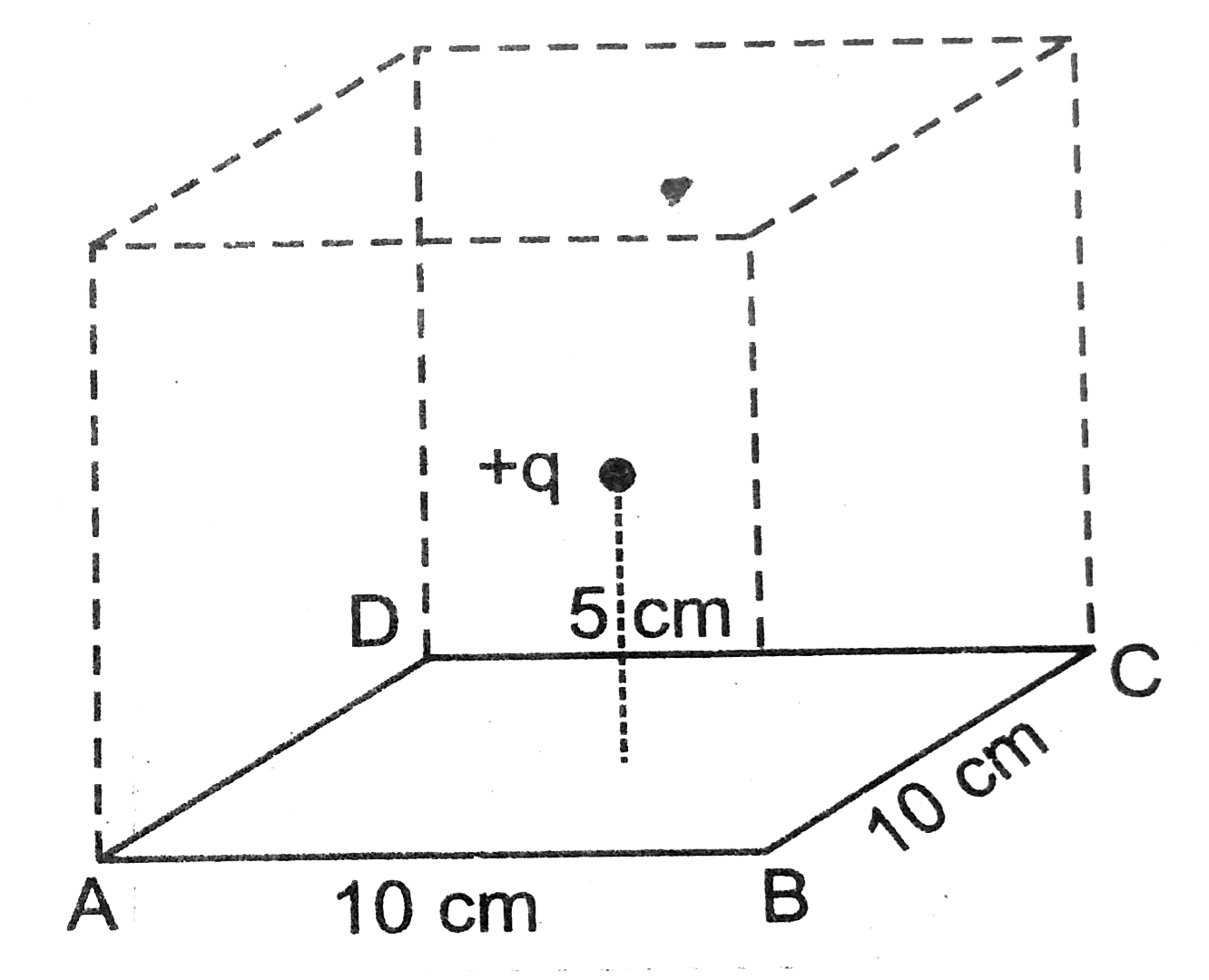
View SolutionA point charge +20muC is at a distance 6 cm directly above the centre of a square of side 12 cm as shown is figure. The magnitude of electric flux through the square is
View SolutionA point charge +10μC is a distance 5 cm directly above the centre of a square of side 10 cm, as shown in fig. What is the magnitude of the electric flux through the square?

View SolutionA point charge of +6μC is placed at a distance 20 cm directly above the centre of a square of side 40 cm . The magnitude of the flux through the square is
View SolutionA point charge of +6mu C is placed at a distance 20 cm directly above the centre of a square of side 40 cm. The magnitude of the flux through the square is
View SolutionA point charge + mu c is a distance 5 cm directly above the centre of a square of side 10 cm as what is the magnitude of the electric flux through the square
View SolutionA point charge + mu c is a distance 5 cm directly above the centre of a square of side 10 cm as what is the magnitude of the electric flux through the square
View SolutionA point charge +10 mu C is at distance of 5cm directly above the center of a square of side 10 cm as shown in Fig. What is the magnitude of the electric flux through the square ? (Hint. Think of the square of the square as one face of a cube with edge 10 cm)
View SolutionA point charges +10 mu C is a distance 5 cm directly above centre of a square of side 10 cm as shown in What is the magnitude of the electric flux through the square?
View SolutionA point charge + 10 mu c is a distance 5 cm directly above the centre of a square of side 10 cm as what is the magnitude of the electric flux through the square
View SolutionA point charge +20muC is at a distance 6 cm directly above the centre of a square of side 12 cm as shown is figure. The magnitude of electric flux through the square is
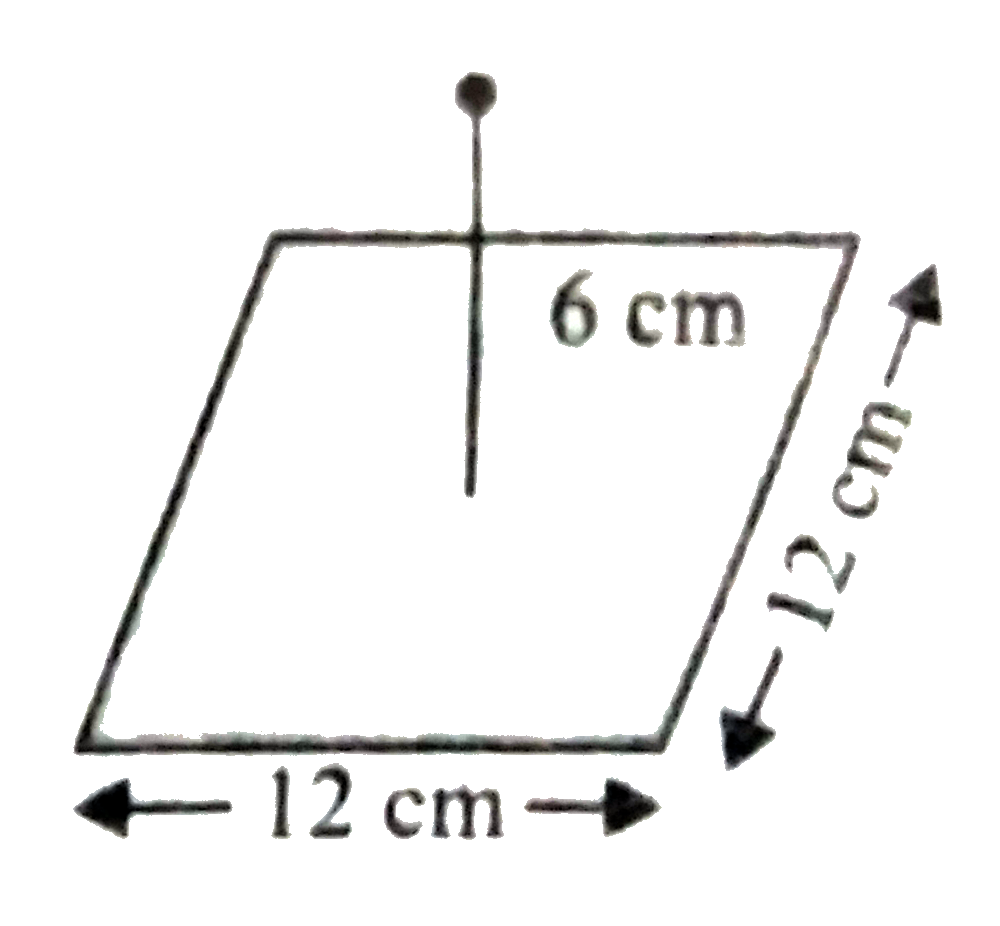
View Solution

