किसी आयताकार निर्देशांक पद्धति में का एक आवेश मूल बिन्दु पर रखा जाता हैं और का आवेश उस बिन्दु पर जहाँ x=6 m और y = 0 हैं। (a) x = 3m, y = 0 और (b) x = 3 m, y = 4 m पर वैद्युत क्षेत्र क्या हैं?
चित्र 2.69 देखें। यहाँ
है।
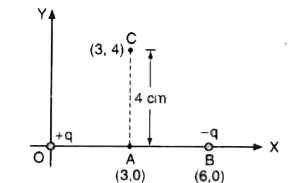
बिन्दु पर आवेश +q के कारण बिन्दु 4 पर वैद्युत क्षेत्र
दिशा में
बिन्दु B पर आवेश -q के कारण बिन्दु A पर वैद्युत क्षेत्र
दिशा में
क्योंकि और एक ही दिशा में हैं, इसलिए आवेशों +q और -q के कारण बिन्दु A पर परिणामी वैद्युत क्षेत्र
या
(b) बिन्दु O पर आवेश +q और बिन्दु B पर आवेश -q से एक वैद्युत द्विध्रुव बनता है जिसका द्विध्रुव आघूर्ण
बिन्दु C, इस द्विध्रुव की निरक्षीय रेखा पर r दूरी पर है, जहाँ r=4cm हैं।
Topper's Solved these Questions
- वैद्युत क्षेत्र और गाउस नियमBOOK - GRB PUBLICATION HINDICHAPTER - वैद्युत क्षेत्र और गाउस नियमEXERCISE - NCERT पाठ्यपुस्तक अभ्यास : उत्तरो सहित
29 Videos
- वैद्युत क्षेत्र और गाउस नियमBOOK - GRB PUBLICATION HINDICHAPTER - वैद्युत क्षेत्र और गाउस नियमEXERCISE - प्रश्नोत्तरी : 5 अंक
3 Videos
- विद्युत परिपथ , विद्युत ऊर्जा और शक्ति BOOK - GRB PUBLICATION HINDICHAPTER - विद्युत परिपथ , विद्युत ऊर्जा और शक्ति EXERCISE - प्रतियोगिता सामग्री ( रिक्त स्थान भरना )
15 Videos
- वैद्युत विभवBOOK - GRB PUBLICATION HINDICHAPTER - वैद्युत विभवEXERCISE - विषय आधारित अभ्यास (प्रतिरूपी अभ्यास)
12 Videos
Similar Questions
हवा में एक दूसरे से 30 cm दूर रने 2×10−7C और 3×10−7C आवेश वाले दो छोटे आवेशित गोलों के बीच बल ज्ञात करें।
View Solution(a) वैद्युत द्विध्रुव आघूर्ण की परिभाषा दें। क्या यह स्केलर है या वेक्टर? द्विध्रुव की निरक्षीय रेखा पर किसी बिन्दु पर इसके वैद्युत क्षेत्र के लिए व्यंजक ट्युत्पन्न करें।
(b) किसी वैद्युत्त द्विधव के कारण समविभव पृष्ठ खींचें। वे बिन्दु ढूँढें जहाँ द्विध्रुव के कारण विभव शून्य है।
View Solutionएक H-परमाणु में एक इलेक्ट्रॉन नाभिक के इर्द-गिर्द 6.6×1015 rps लगाता है। तुल्य धारा ..............A है।
View Solutionपृथ्वी पर किसी जगह आसमानी बिजली गिरती है और 1.00×108V के विभवान्तर पर बादल से पृथ्वी को -20.0 C का आवेश देती है।
(a) क्या बादल उच्च विभव पर है या पृथ्वी?
(b) पृथ्वी को कितनी ऊर्जा दी जाती है?
(c) यदि इस ऊर्जा को एक 100 W के बिजली के बल्ब को जलाने के लिए प्रयोग किया जा सकता, तो यह कितने दिन चलेगी?
View Solutionयदि वक्र y=x3+ax−b के बिन्दु (1,−5) पर खींची गई स्पर्श रेखा , −x+y+4=0 रेखा पर लम्बवत हैं , तो निम्न में से कोण-सा एक बिन्दु वक्र पर स्थित हैं ?
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionयदि a, b और c समान्तर श्रेढ़ी में हैं, तो ax+by+c=0 एक नियत बिन्दु से होकर जाएगी , जिसके निर्देशांक ............. हैं।
View Solutionबिन्दु (1,1) पर वक्रों y=x2 और x=y2 के मध्य कोण है
View Solutionयदि वक्र y=ax और y=bx एक दूसरे को α कोण पर काटते हैं, तब tanα का मान है
View Solutionवृत्त x2+y2−2x−4y+3=0 का बिन्दु (2,3) पर अभिलम्ब वृत्त x2+y2=1 को बिन्दु P और Q पर प्रतिच्छेद करता है। व्यास PQ वाले वृत्त का क्षेत्रफल है
View Solutionएक बिन्दु पर क्रियाशील दो बल P और Q का अधिकतम परिणामी बल ........ होता है।
View Solutionएक बिन्दु पर क्रियाशील दो बल 8N और 12N का अधिकतम परिणामी बल ____ होगा।
View Solutionगतिमान आवेश और चुंबकत्व पर महत्वपूर्ण प्रश्न
View Solutionदो अनन्त लम्बाई के समान्तर तार जिन पर रेखीय आवेश घनत्व क्रमश: λ1, औरλ2 , हैं R मीटर की दूरी पर रखे हैं, उनमें से किसी एक की एकांक लम्बाई पर बल होगा
View Solution
