Rays parallel to principal axis, incident on the spherical mirror at different heights from principal axis are focused at different points. And due to this reason we cannot define unique focus. This is known as spherical aberration. Angle of incidence $θ$ shown in figure depends on the height of ray above principal axis. Focal length of spherical mirror can be easily written in terms of angle $θ$ shown in figure as follows :
$f = R - \frac{R}{2} sec θ$
Here R is radius of curvature of mirror. The light rays which are very close to principal axis are known as paraxial rays and rays far away from principal axis are called marginal rays.
What will be the focal length for ray which is incident at an angle $60^{\circ}$ ?

What will be the focal length for ray which is incident at an angle $60^{\circ}$ ?

$R / 2$

Video Solution

Text Solution

Verified by Experts

We can substitute value of $θ$ in given formula.
$f = R - \frac{R}{2} {sec 60}^{\circ} = R - R = 0$

Updated on:21/07/2023

Class 12 PHYSICS GEOMETRICAL OPTICS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One

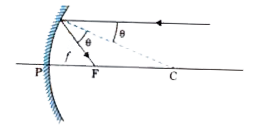
Rays parallel to principal axis, incident on the spherical mirror at different heights from principal axis are focused at different points. And due to this reason we cannot define unique focus. This is known as spherical aberration. Angle of incidence $θ$ shown in figure depends on the height of ray above principal axis. Focal length of spherical mirror can be easily written in terms of angle $θ$ shown in figure as follows :
$f = R - \frac{R}{2} sec θ$
Here R is radius of curvature of mirror. The light rays which are very close to principal axis are known as paraxial rays and rays far away from principal axis are called marginal rays.
For paraxial rays focal length is approximately
AFor paraxial rays focal length is approximately
B2R
C $R / 2$
D4R
Question 2 - Select One

Rays parallel to principal axis, incident on the spherical mirror at different heights from principal axis are focused at different points. And due to this reason we cannot define unique focus. This is known as spherical aberration. Angle of incidence $θ$ shown in figure depends on the height of ray above principal axis. Focal length of spherical mirror can be easily written in terms of angle $θ$ shown in figure as follows :
$f = R - \frac{R}{2} sec θ$
Here R is radius of curvature of mirror. The light rays which are very close to principal axis are known as paraxial rays and rays far away from principal axis are called marginal rays.
Let $f_{P}$ and fm represent the focal length corresponding to paraxial rays and marginal rays respectively then
ALet $f_{p}$ and fm represent the focal length corresponding to paraxial rays and marginal rays respectively then
B $f_{p} = f_{m}$
C $f_{p} > f_{m}$
D $f_{p} < f_{m}$
Question 3 - Select One
STATEMENT- $1$ Law of reflection is applicable for all type of mirrors.
$S T A T E M E N T 2$ Rays which are parallel to principal axis are known as paraxial rays.
ASTATEMENT - $1$ is true statement $2$ is true,Statement - $2$ is a correct explanation for statement - $1$
BSTATEMENT - $1$ is true statement $2$ is true,Statement - $2$ is a not a correct explanation for statement - $1$
CStatement - $1$ is true,Statement - $2$ is False
DStatement - $1$ is False ,Statement - $2$ is True

MODERN PUBLICATION-RAY OPTICS AND OPTICAL INSTRUMENTS-OBJECTIVE TYPE QUESTIONS (D. MULTIPLE CHOICE QUESTIONS)

Home
Ask Doubt
Profile

We can substitute value of θ in given formula. f=R−R2sec60∘=R−R=0

Topper's Solved these Questions

Similar Questions

Knowledge Check

STATEMENT-1 Law of reflection is applicable for all type of mirrors. STATEMENT2Rays which are parallel to principal axis are known as paraxial rays.

MODERN PUBLICATION-RAY OPTICS AND OPTICAL INSTRUMENTS-OBJECTIVE TYPE QUESTIONS (D. MULTIPLE CHOICE QUESTIONS)

We can substitute value of $θ$ in given formula.
$f = R - \frac{R}{2} {sec 60}^{\circ} = R - R = 0$

STATEMENT- $1$ Law of reflection is applicable for all type of mirrors.
$S T A T E M E N T 2$ Rays which are parallel to principal axis are known as paraxial rays.