Distance between a candle and screen is D. A convex lens of focal length 20 cm is brought in between them and it is found that real image of candle can be formed on the screen for some position of lens.
D must be less than or equal to 80 cm
D must be greater than or equal to 80 cm
D may be less than 160 cm
D may be greater than 160 cm
The correct Answer is:B, C, D
To solve the problem, we need to analyze the situation involving a candle, a convex lens, and a screen. The distance between the candle and the screen is given as D, and the focal length of the convex lens is f=20cm. We want to determine the possible values of D for which a real image of the candle can be formed on the screen.
1. Understanding the Lens Formula:
The lens formula relates the object distance u, image distance v, and focal length f of a lens:
1f=1v−1u
2. Identifying Object and Image Positions:
- Let the distance from the candle to the lens be u.
- The distance from the lens to the screen will then be D−u.
- The image distance v can be expressed as D−u.
3. Substituting into the Lens Formula:
Substitute v into the lens formula:
120=1D−u−1u
4. Rearranging the Equation:
Rearranging gives:
1D−u=120+1u
This can be further simplified to:
1D−u=u+2020u
5. Cross-Multiplying:
Cross-multiplying yields:
20u=(D−u)(u+20)
6. Expanding and Rearranging:
Expanding the right side:
20u=Du+20D−u2−20u
Rearranging gives:
u2+(D−40)u+20D=0
7. Using the Discriminant:
For the quadratic equation u2+(D−40)u+20D=0 to have real solutions, the discriminant must be non-negative:
(D−40)2−80D≥0
8. Simplifying the Discriminant:
Simplifying the discriminant:
D2−80D+1600≥0
This can be factored or solved using the quadratic formula.
9. Finding the Roots:
The roots of the equation D2−80D+1600=0 are:
D=80±√02=40
Since the discriminant is zero, the equation has a double root at D=80.
10. Analyzing the Inequality:
The quadratic opens upwards, so the solution to the inequality is:
D≤80orD≥80
Thus, D can be any value greater than or equal to 80cm.
Conclusion:
The distance D between the candle and the screen must be greater than or equal to 80cm for a real image to be formed on the screen by the convex lens.
The lens formula relates the object distance u, image distance v, and focal length f of a lens:
1f=1v−1u
- Let the distance from the candle to the lens be u.
- The distance from the lens to the screen will then be D−u.
- The image distance v can be expressed as D−u.
Substitute v into the lens formula:
120=1D−u−1u
Rearranging gives:
1D−u=120+1u
This can be further simplified to:
1D−u=u+2020u
Cross-multiplying yields:
20u=(D−u)(u+20)
Expanding the right side:
20u=Du+20D−u2−20u
Rearranging gives:
u2+(D−40)u+20D=0
For the quadratic equation u2+(D−40)u+20D=0 to have real solutions, the discriminant must be non-negative:
(D−40)2−80D≥0
Simplifying the discriminant:
D2−80D+1600≥0
This can be factored or solved using the quadratic formula.
The roots of the equation D2−80D+1600=0 are:
D=80±√02=40
Since the discriminant is zero, the equation has a double root at D=80.
The quadratic opens upwards, so the solution to the inequality is:
D≤80orD≥80
Thus, D can be any value greater than or equal to 80cm.
The distance D between the candle and the screen must be greater than or equal to 80cm for a real image to be formed on the screen by the convex lens.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:MODERN PUBLICATIONChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:OBJECTIVE TYPE QUESTIONS (D. MULTIPLE CHOICE QUESTIONS)
Explore 5 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:MODERN PUBLICATIONChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS)
Explore 10 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:MODERN PUBLICATIONChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:OBJECTIVE TYPE QUESTIONS (JEE (ADVANCED) FOR IIT ENTRANCE)
Explore 20 Videos
- NUCLEIBook:MODERN PUBLICATIONChapter:NUCLEIExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Book:MODERN PUBLICATIONChapter:SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Exercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 12 Videos
Similar Questions
An object is placed at a certain distance from a screen. A convex lens of focal length 20cm is placed between the screen and the object. A real image is formed on the screen for two positions of the lens, which differ by a distance of 10cm. What is the distance of the object from the screen ?
View SolutionDistance between a fixed linear object and a fixed screen is 40cm .A thin convex lens of focal length 10cm is kept between object and screen such that object is perpendicular to the principal axis of lens as shown in figure.It is observed that for two different positions of lens images are formed on the screen.If size of images for the two different positions of lens are 9cm and 4cm then size of object in cm is......
View Solution
Knowledge Check
The distance between an electric lamp and a screen is d=1m. A convergent lens of focal length f=21cm is placed between the lamp and the lens such that a sharp image of the lamp filament is formed on the screen.
AThe positions of the lens from the lamp for which sharp images are formed on the screen are 35cm and 65cm.BThe positions of the lens from the lamp for which sharp images are formed on the screen are 35cm and 70cmCMagnitude of the difference in magnification is 40/21DThe size of the lamp filament for which there are two sharp images of 4.5cm and 2cm, is 3cmAn object and a screen are kept at a distance of 120 cm A lens of focal length 22.5 cm is kept between them so that a real image is formed on the screen Find the possible location (s) of the lens.
A90cm from objectB30cm from objectC40cm from objectD80cm from objectA luminous object and a screen are at a fixed distance D apart. A converging lens of focal length f is placed between the object and screen. A real image of the object in formed on the screen for two lens positins if they are separated by a distance d equal to
A√D(D+4F)B√D(D−4F)C√2D(D−4F)D√D2+4F
A convex lens when placed in the first position forms a real image of an object on a fixed screen. The distance between the object and the screen is 75 cm. On displacing the lens from first position by 25 cm to the second position, again a real image is formed on the screen. Then the focal length of the lens is
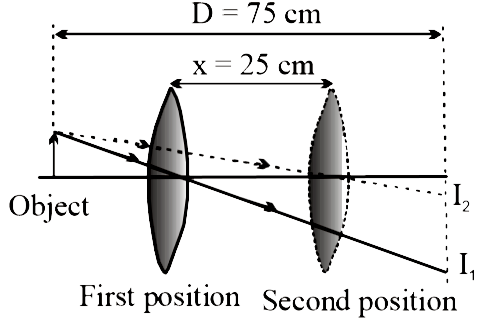
View SolutionAn object 2 cm high is placed at a distance of 64 cm from a white screen. On placing a convex lens at a distance of 32 cm from the object it is found that a distinct image of the object is formed on the screen. What is the focal length of the convex lens and size of the image formed on the screen ?
View SolutionScreen is placed at a distance 60 cm from an object. A convex lens of focal length f is placed between object and screen and it is attempted that real image of object is formed on the screen. But real image could not be formed for any position of lens between object and screen.
View SolutionThe distance between an object and the screen is 75 cm. When a convex lens of focal length 12 cm is placed in the between theobject and the screen, magnification of real formed can be (magnitude only)
View SolutionThe distance between the object and the screen is d (greater than 4 times the focal length of a convex lens). Real images of the object are obtained on the screen for two positions of the lens that are separated by distance x apart. The ratio of size of the images in the two positions of the lens are
View Solution

