A glass lens of refractive index 1.5 is placed in a trough of liquid. What must be the refractive index of the liquid in order to make the lens disappear ?

Video Solution

Text Solution

Generated By DoubtnutGPT

To determine the refractive index of the liquid required to make a glass lens of refractive index 1.5 disappear, we can follow these steps:
Step 1: Understand the Concept of Invisibility
For an object to appear invisible, the light must not refract or reflect when it passes through the object. This occurs when the refractive index of the object is equal to the refractive index of the surrounding medium.
Hint: Think about how light behaves when it passes from one medium to another.
Step 2: Identify the Refractive Indices
In this case, we have:
- Refractive index of the glass lens (n_glass) = 1.5
- Refractive index of the liquid (n_liquid) = ?
Hint: The condition for invisibility is that the refractive indices must match.
Step 3: Set the Condition for Invisibility
For the lens to disappear, the refractive index of the liquid must be equal to the refractive index of the glass lens. Therefore, we can write the equation:
$n_{l i q u i d} = n_{g l a s s}$
Hint: This equation shows that the two refractive indices must be equal.
Step 4: Substitute the Known Values
Substituting the known value of the refractive index of the glass lens into the equation gives us:
$n_{l i q u i d} = 1.5$
Hint: You are directly substituting the value you have for the glass lens.
Step 5: Conclusion
Thus, the refractive index of the liquid must be 1.5 for the glass lens to become invisible.
Final Answer: The refractive index of the liquid should be 1.5.
---

Updated on:7/8/2024

When a lens of refractive index $n_{1}$ is placed in a liquid of refractive index $n_{2}$ , the lens looks to be disappeared only if
A $n_{1} = \frac{n_{2}}{2}$
B $n_{1} = \frac{3}{4} n_{2}$
C $n_{1} = n_{2}$
D $n_{1} = \frac{5}{4} n_{2}$
An equiconvex lens of refractive index $n_{2}$ is placed such that the refractive index of the surrouding media is as shown. The lens :

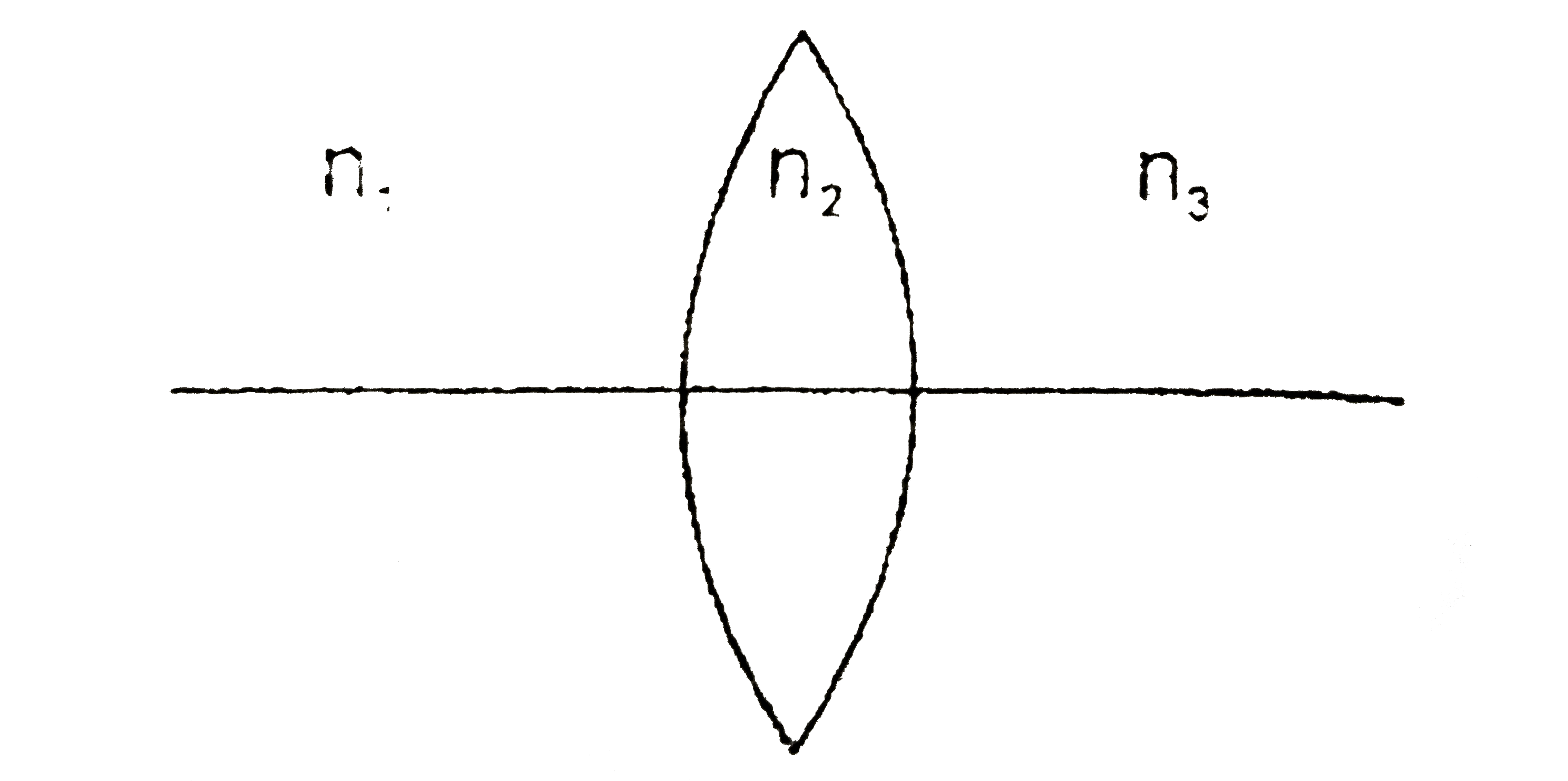Amust be diverging if $n_{2}$ is less than the aritmetic mean of $n_{1}$ and $n_{3}$
Bmust be converging if $n_{2}$ is greater than the arithmetic mean of $n_{1}$ and $n_{3}$
Cmay be diverging if $n_{2}$ is less than the arihmetic mean of $n_{1}$ and $n_{3}$
Dwill neither be diverging nor converging if $n_{2}$ is equal to arithmetic mean of $n_{1}$ and $n_{3}$