A concave lens is cut vertically into two equal parts. What will be the focal length of each plano-concave lens obtained ?
To find the focal length of each plano-concave lens obtained by vertically cutting a concave lens into two equal parts, we can follow these steps:
Step 1: Understand the Original Lens
The original lens is a concave lens, which has a focal length denoted as f1. The lensmaker's formula for a lens is given by:
1f=(μ−1)(1r1−1r2)
Where:
- μ is the refractive index of the lens material.
- r1 is the radius of curvature of the first surface (concave surface).
- r2 is the radius of curvature of the second surface (convex surface).
Step 2: Apply the Lensmaker's Formula
For the original concave lens:
- Let’s assume the radius of curvature of both surfaces is r.
- The first surface (concave) will have r1=−r (negative because it is concave).
- The second surface (convex) will have r2=+r.
Substituting these values into the lensmaker's formula:
1f1=(μ−1)(1−r−1r)
This simplifies to:
1f1=(μ−1)(−2r)
Thus,
f1=−r2(μ−1)
Step 3: Cut the Lens Vertically
When the concave lens is cut vertically into two equal parts, each part becomes a plano-concave lens. For each of these lenses:
- One surface is flat (plane), and the other surface remains concave.
Step 4: Analyze the New Lens
For the new plano-concave lens:
- The radius of curvature for the plane surface r2 tends to infinity, so 1r2=0.
- The radius of curvature for the concave surface remains r1=−r.
Substituting these into the lensmaker's formula for the new lens:
1f2=(μ−1)(1−r−0)
This simplifies to:
1f2=−μ−1r
Thus,
f2=−rμ−1
Step 5: Relate the Focal Lengths
From our earlier calculations, we have:
f1=−r2(μ−1)
And now we have:
f2=−rμ−1
Step 6: Conclusion
Comparing f2 with f1:
f2=2f1
This means the focal length of each plano-concave lens obtained is double that of the original concave lens.
Final Answer
The focal length of each plano-concave lens obtained is 2f1.
---
The original lens is a concave lens, which has a focal length denoted as f1. The lensmaker's formula for a lens is given by:
- μ is the refractive index of the lens material.
- r1 is the radius of curvature of the first surface (concave surface).
- r2 is the radius of curvature of the second surface (convex surface).
For the original concave lens:
- Let’s assume the radius of curvature of both surfaces is r.
- The first surface (concave) will have r1=−r (negative because it is concave).
- The second surface (convex) will have r2=+r.
When the concave lens is cut vertically into two equal parts, each part becomes a plano-concave lens. For each of these lenses:
- One surface is flat (plane), and the other surface remains concave.
For the new plano-concave lens:
- The radius of curvature for the plane surface r2 tends to infinity, so 1r2=0.
- The radius of curvature for the concave surface remains r1=−r.
From our earlier calculations, we have:
Comparing f2 with f1:
The focal length of each plano-concave lens obtained is 2f1.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:MODERN PUBLICATIONChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:Tough & Tricky (PROBLEMS)
Explore 20 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:MODERN PUBLICATIONChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:NCERT FILE SOLVED (TEXT BOOK EXERCISES)
Explore 38 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:MODERN PUBLICATIONChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:PRACTICE PROBLEMS (11)
Explore 4 Videos
- NUCLEIBook:MODERN PUBLICATIONChapter:NUCLEIExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Book:MODERN PUBLICATIONChapter:SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Exercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 12 Videos
Similar Questions
Knowledge Check
A convex lens has its radi of curvature equal. The focal length of the lens is f. It is is dividded vertically into two identical plano-convex lenses by cutting it, then the focal length of the plane -convex lens is (μ= the refractive index of the material of the lens)
AfBf2C2fD(μ−1)fA convex lens of focal length 10 cm is in contact with a concave lens. The focal length of the combination is numerically equal to that of the concave lens. The focal length of the concave lens is
A10 cmB15 cmC5 cmD20 cmA biconcave lens of power P vertically splits into two identical plano concave parts. The power of each part will be
A2PBP2CPDP√2
If the convex lens of focal length 10 cm and a concave lens of focal length 50 cm are kept in contact with each other.
What will be the focal length of the combination ?
View SolutionIf a convex lens of focal length 20 cm and a concave lens of focal length 30 cm are kept in contract with each other.
What will be the focal length of the combination ?
View SolutionFrom the ray diagram shown in Fig. calculte the focal length of concave lens.
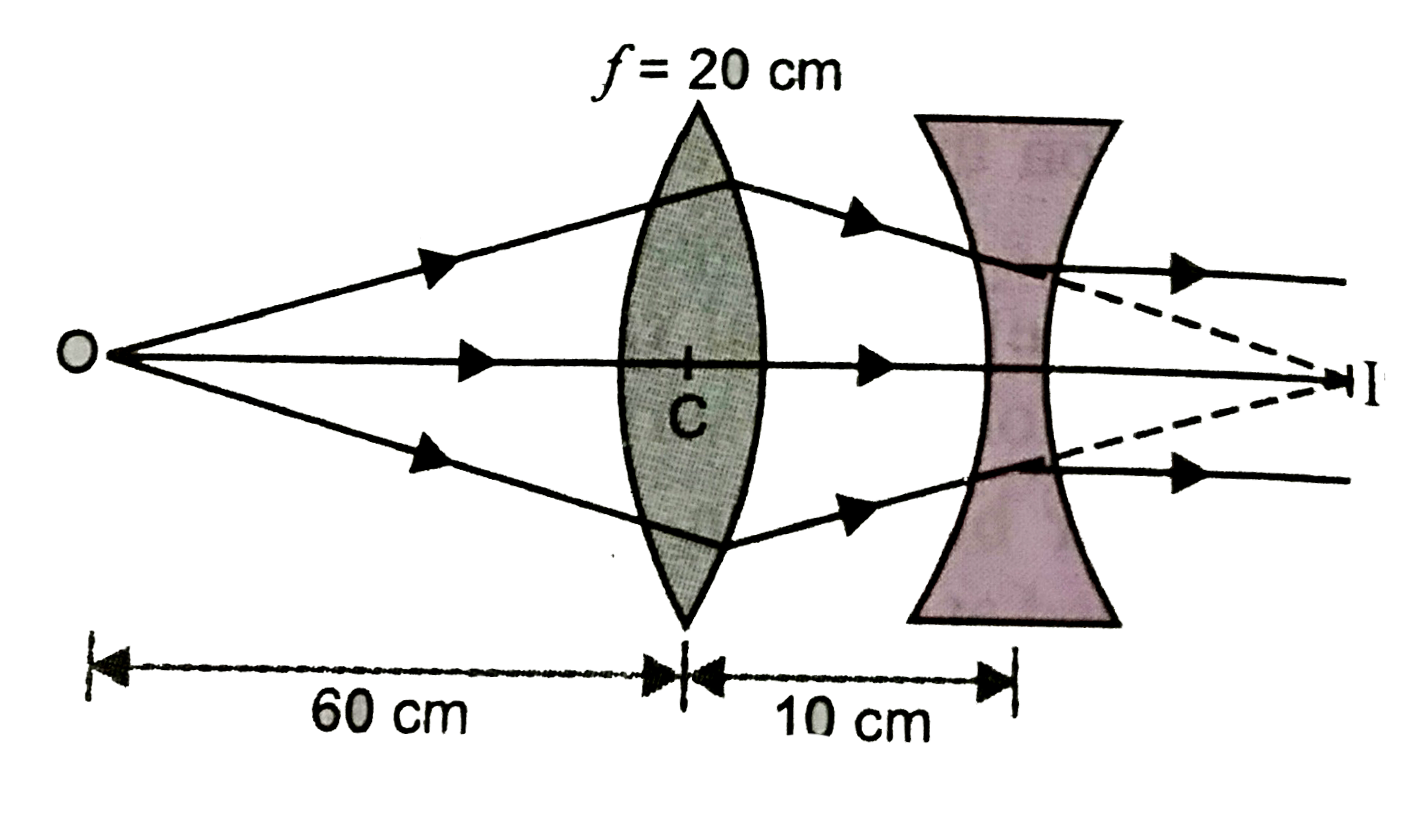 .
.
View SolutionIf a convex lens of focal length 10 cm and a concave lens of focal length 50 cm are kept in contact with each other , (i) what will be the focal length of the combination ? (ii) What will be the power of the combination? (iii) What will be the behaviour of the combination ( behaviour as a convex lens / concave lens ) ?
View SolutionFocal length of convex lens is f. If this lens is cut along parallel to its length in two equal parts then focal length of its half part will be:
View Solution

