A concave mirror has a focal length f. An object of height 1 cm is placed perpendicular to the principal axis in front of the mirror at a distance of 2 f. Calculate the height and nature of the image formed.
To solve the problem, we will follow these steps:
Step 1: Understand the given information
We have a concave mirror with a focal length f. An object of height ho=1 cm is placed at a distance u=−2f (the negative sign indicates that the object is in front of the mirror).
Step 2: Use the mirror formula
The mirror formula is given by:
1f=1v+1u
where:
- f is the focal length of the mirror,
- v is the image distance,
- u is the object distance.
Step 3: Substitute the values into the mirror formula
Since the focal length of a concave mirror is negative, we have:
1−f=1v+1−2f
Step 4: Rearrange the equation to find v
Rearranging the equation gives:
1v=1−f+12f
1v=−1f+12f=−22f+12f=−12f
Taking the reciprocal, we find:
v=−2f
Step 5: Determine the nature of the image
Since v is negative, this indicates that the image is formed on the same side as the object, which means it is a real image.
Step 6: Calculate the magnification
The magnification M is given by:
M=−vu
Substituting the values:
M=−−2f−2f=−1
Step 7: Calculate the height of the image
The height of the image hi can be calculated using the magnification formula:
M=hiho
Substituting the known values:
−1=hi1
This gives:
hi=−1 cm
Step 8: Conclusion
The height of the image is 1 cm, and since it is negative, it indicates that the image is inverted. Thus, the image is real, inverted, and has a height of 1 cm.
Final Answer
The height of the image is 1 cm and the nature of the image is real and inverted.
---
We have a concave mirror with a focal length f. An object of height ho=1 cm is placed at a distance u=−2f (the negative sign indicates that the object is in front of the mirror).
The mirror formula is given by:
1f=1v+1u
where:
- f is the focal length of the mirror,
- v is the image distance,
- u is the object distance.
Since the focal length of a concave mirror is negative, we have:
1−f=1v+1−2f
Rearranging the equation gives:
1v=1−f+12f
1v=−1f+12f=−22f+12f=−12f
Taking the reciprocal, we find:
v=−2f
Since v is negative, this indicates that the image is formed on the same side as the object, which means it is a real image.
The magnification M is given by:
M=−vu
Substituting the values:
M=−−2f−2f=−1
The height of the image hi can be calculated using the magnification formula:
M=hiho
Substituting the known values:
−1=hi1
This gives:
hi=−1 cm
The height of the image is 1 cm, and since it is negative, it indicates that the image is inverted. Thus, the image is real, inverted, and has a height of 1 cm.
The height of the image is 1 cm and the nature of the image is real and inverted.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:MODERN PUBLICATIONChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:PRACTICE PROBLEMS (2)
Explore 9 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:MODERN PUBLICATIONChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:PRACTICE PROBLEMS (3)
Explore 18 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:MODERN PUBLICATIONChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
- NUCLEIBook:MODERN PUBLICATIONChapter:NUCLEIExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Book:MODERN PUBLICATIONChapter:SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Exercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 12 Videos
Similar Questions
Shown in Fig. is a vertically erect object placed on the optic axis at a distance (5/2)f from a concave mirror of focal length f. If a plane mirror is placed perpendicular to the optic axis at a distanc (4/3)f from the pole, facing concave mirror, find the position and nature of the final image formed.
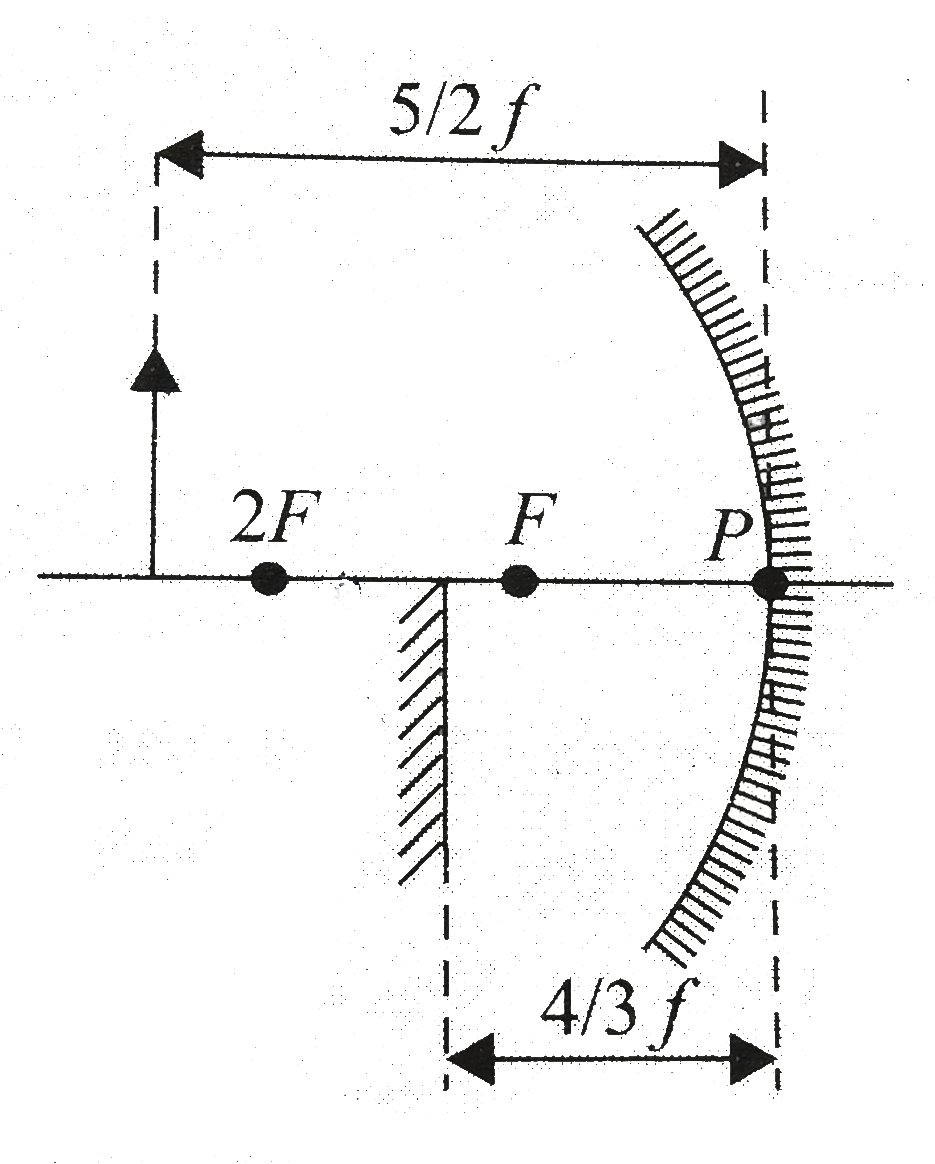
View Solution(a) An object of height 2.5 cm is placed perpendicularly on the principal axis of a concave mirror of focal length f at a distance of 34f. What will be the nature of the image of the object and its height ?
(b) A person uses spectacles of power +2D. What type of defect of vision is it ?
View Solution
Knowledge Check
An object of size 2.0 cm is placed perpendicular to the principal axis of a concave mirror. The distance of the object from the mirror equals the radius of curvature. The size of the image will be
A0.5 cmB1.0 cmC1.5 cmD2.0 cmA convex mirror has a focal length f. A real object is placed at a distance f in front of it from the pole produces an image at
AinfinityBfCf2D2fA convex mirror has a focal length f. A real object is placed at a distance f in front of it from the pole produces an image at
AInfinityBfCf/2D2f
A 1 cm object is placed perpendicular to the principal axis of a convex mirror of focal length 7.5 cm. Find its distance from the mirror if the image formed is 0.6 cm in size.
View SolutionA convex mirror has a focal length f. A real object is placed at a distance f in front of it from the pole produces an image at
View SolutionAn object of length 6 cm is placed on the principle axis of a concave mirror of focal length f at a distance of 4 f . The length of the image will be
View SolutionAn object is placed on principal axis of concave mirror at distance of 1.5 f Image will be at
View SolutionAn object is placed on the principal axis of a concave mirror at a distance of 1.5 f(f is the focal length). The image will be at,
View Solution

