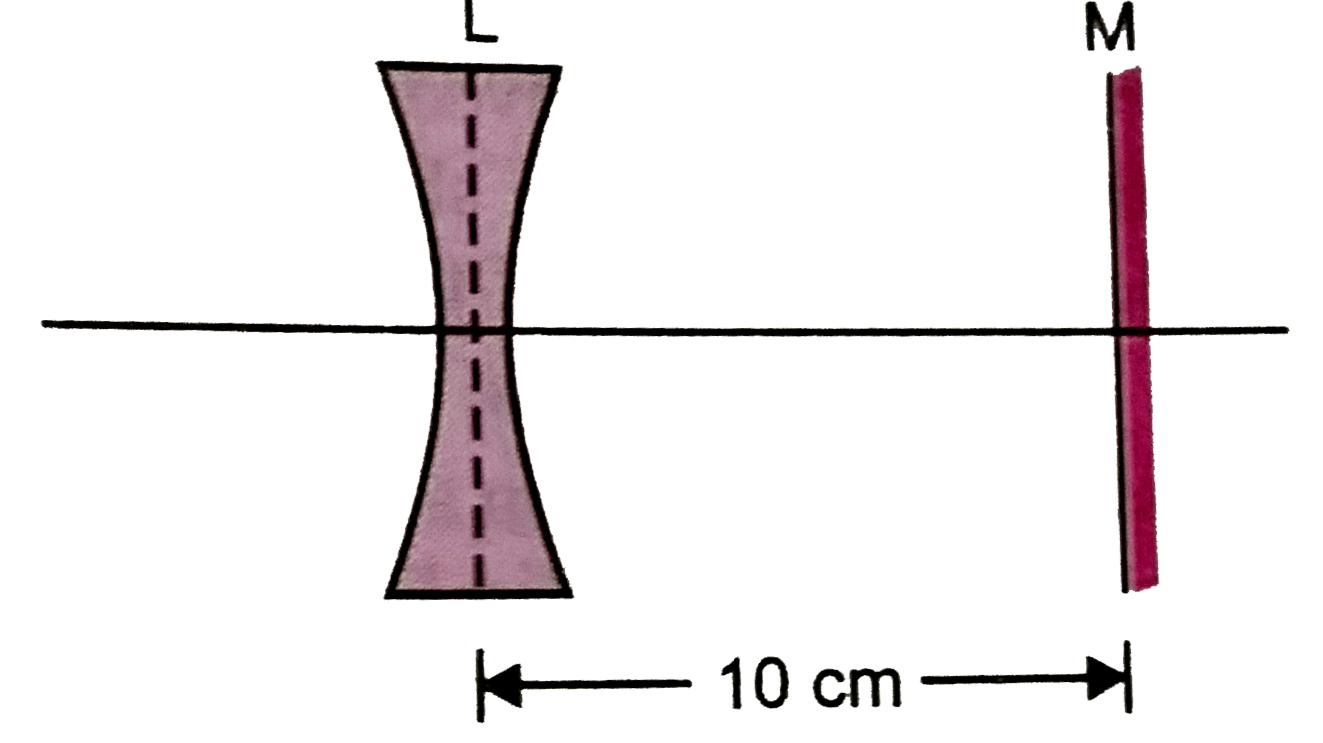
A concave lens and a plane mirror re placed coaxially 10 cm apart. A point object is placed at a distance of 40 cm from the concave lens. The final image formed by the combination is located 30 cm behind the mirror. Calculate the focal length of the concave lens.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

ocr_image
From figure. For the concave lens,
Object distance, u = - 40 c m
Image distance, u = - ( I 1 M - P M )
= - ( 30 - 10 ) = - 20 c m
∴ From lens formula
1 f = 1 v - 1 u
= 1 ( - 20 ) - ( 1 - 40 )
= 1 40 - 1 20 = - 1 40
⇒ f = - 40 c m

Updated on:21/07/2023
|
Class 12PHYSICSGEOMETRICAL OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • An object is placed at a distance of 30 cm from a concave mirror and its real image is formed at a distance of 30 cm from the mirror. The focal length of the mirror is

    A15 cm
    B45 cm
    C30 cm
    D20 cm

  • A convex lens of focal length 30 cm , a concave lens of focal length 120 cm , and a plane mirror are arranged as shown . For an object kept at a distance of 60 cm from the convex lens, the final image, formed by the combination , is a real image , at a distance of :
    ocr_image
    |Focal length|=|Focal length|
    = 30cm =120cm
    ocr_image

    A70 cm from the convex lens
    B60 cm from the convex lens
    C60 cm from the concave lens
    D70 cm from the concave lens

  • An object is placed 40 cm from a concave mirror of focal length 20 cm. The image formed is

    AReal, inverted and same in size
    BReal, inverted and smaller
    CVirtual, erect and larger
    DVirtual, erect and smaller