Derive an expression for the variation of g with the height from the surface of the Earth.
To derive the expression for the variation of gravitational acceleration g with height h from the surface of the Earth, we can follow these steps:
Step 1: Understand the gravitational force
The gravitational force F acting on a body of mass m at a height h from the surface of the Earth can be expressed using Newton's law of gravitation:
F=GMm(R+h)2
where:
- G is the universal gravitational constant,
- M is the mass of the Earth,
- R is the radius of the Earth,
- h is the height above the Earth's surface.
Step 2: Relate force to acceleration
According to Newton's second law, the acceleration a of the body is given by:
a=Fm
Substituting the expression for F:
a=GM(R+h)2
This acceleration a is also known as the acceleration due to gravity at height h, denoted as g′:
g′=GM(R+h)2
Step 3: Express g′ in terms of g
The acceleration due to gravity at the surface of the Earth g is given by:
g=GMR2
Now, we can express g′ in terms of g:
g′=g⋅R2(R+h)2
Step 4: Simplify the expression
Now, we can simplify the expression for g′:
g′=g⋅R2(R+h)2
Step 5: Use the binomial approximation
If h is much smaller than R (i.e., hR≪1), we can use the binomial approximation:
1(1+x)n≈1−nxfor small x
In our case, let x=hR and n=2:
g′≈g⋅(1−2hR)
Thus, we can write:
g′≈g(1−2hR)
Final Expression
The final expression for the variation of g with height h from the surface of the Earth is:
g′≈g(1−2hR)
The gravitational force F acting on a body of mass m at a height h from the surface of the Earth can be expressed using Newton's law of gravitation:
- G is the universal gravitational constant,
- M is the mass of the Earth,
- R is the radius of the Earth,
- h is the height above the Earth's surface.
According to Newton's second law, the acceleration a of the body is given by:
The acceleration due to gravity at the surface of the Earth g is given by:
Now, we can simplify the expression for g′:
If h is much smaller than R (i.e., hR≪1), we can use the binomial approximation:
The final expression for the variation of g with height h from the surface of the Earth is:
Topper's Solved these Questions
Similar Questions
Knowledge Check
The graph that represents variation of g with height (h) from the surface of the earth is
A B
B C
C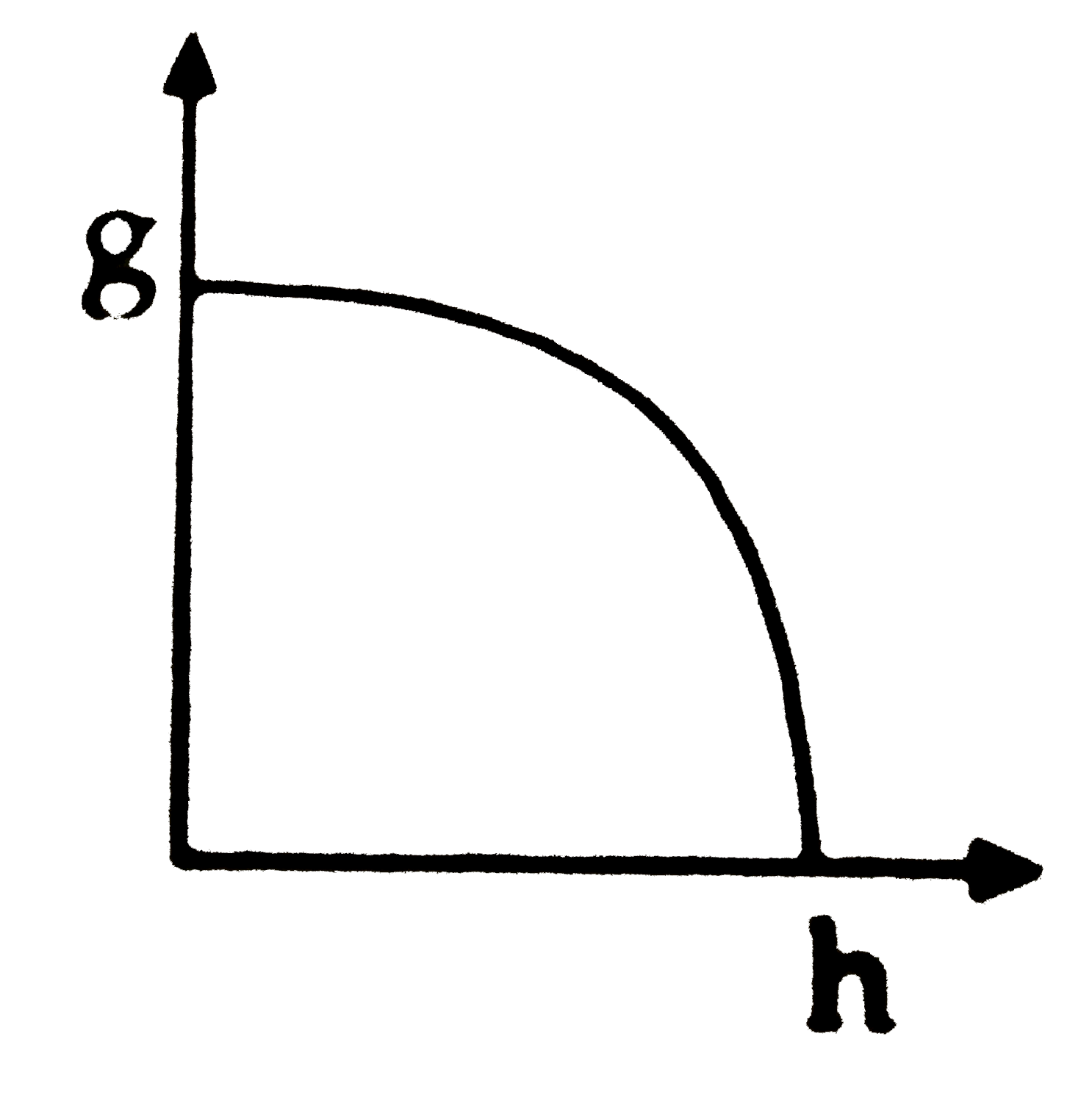 D
D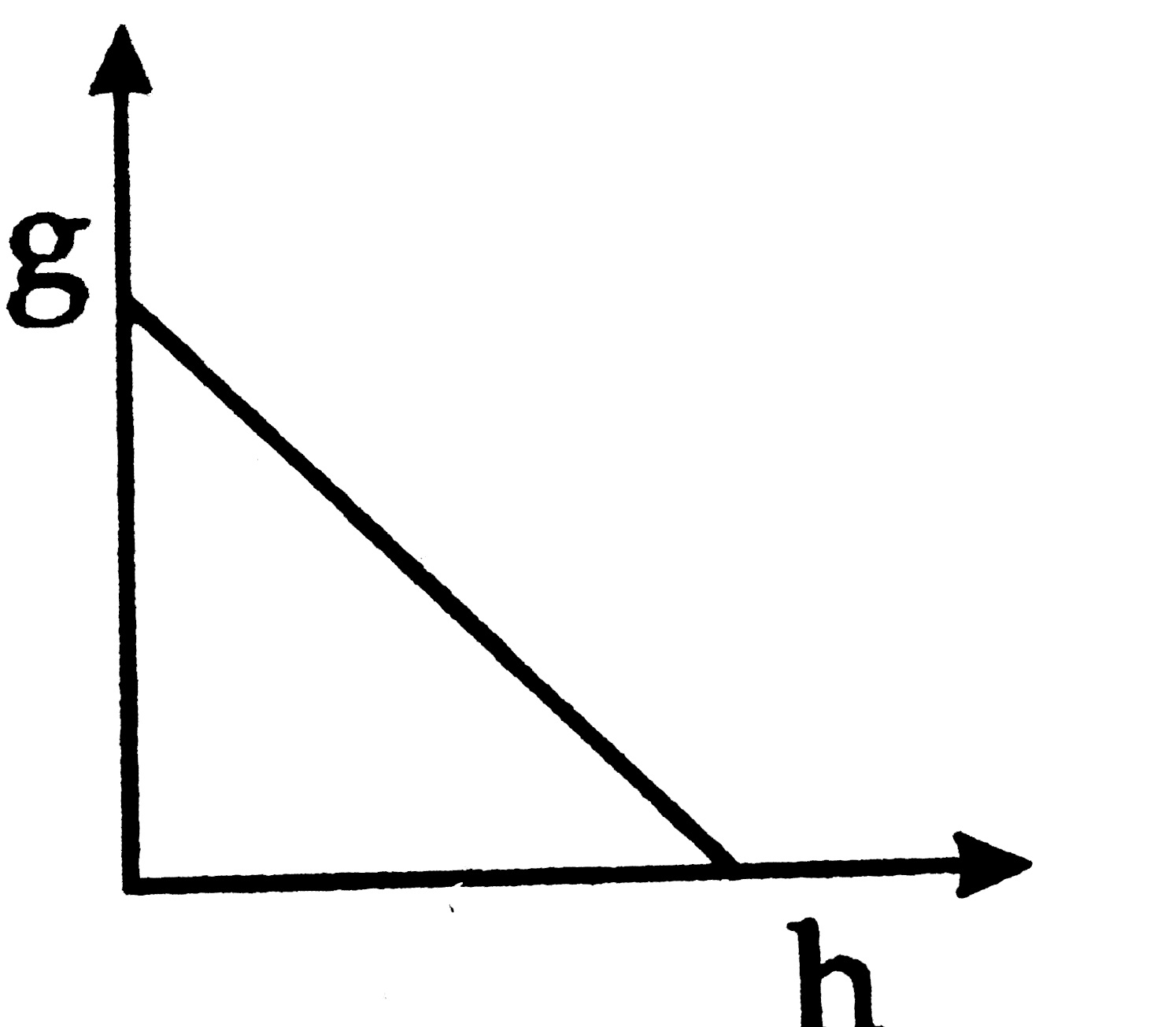
The graph that represents variation of g with depth (d) from the surface of the earth is
A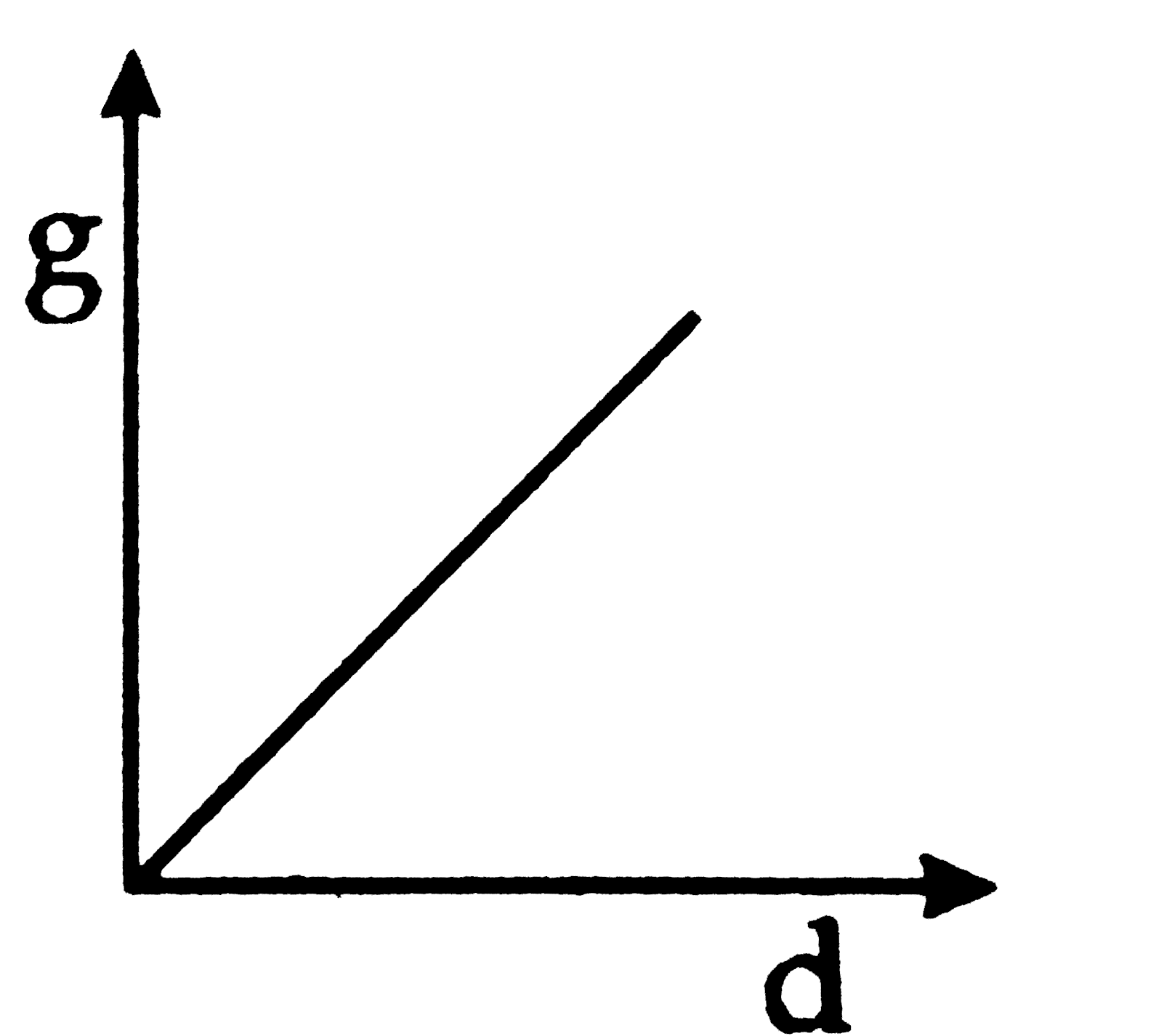 B
B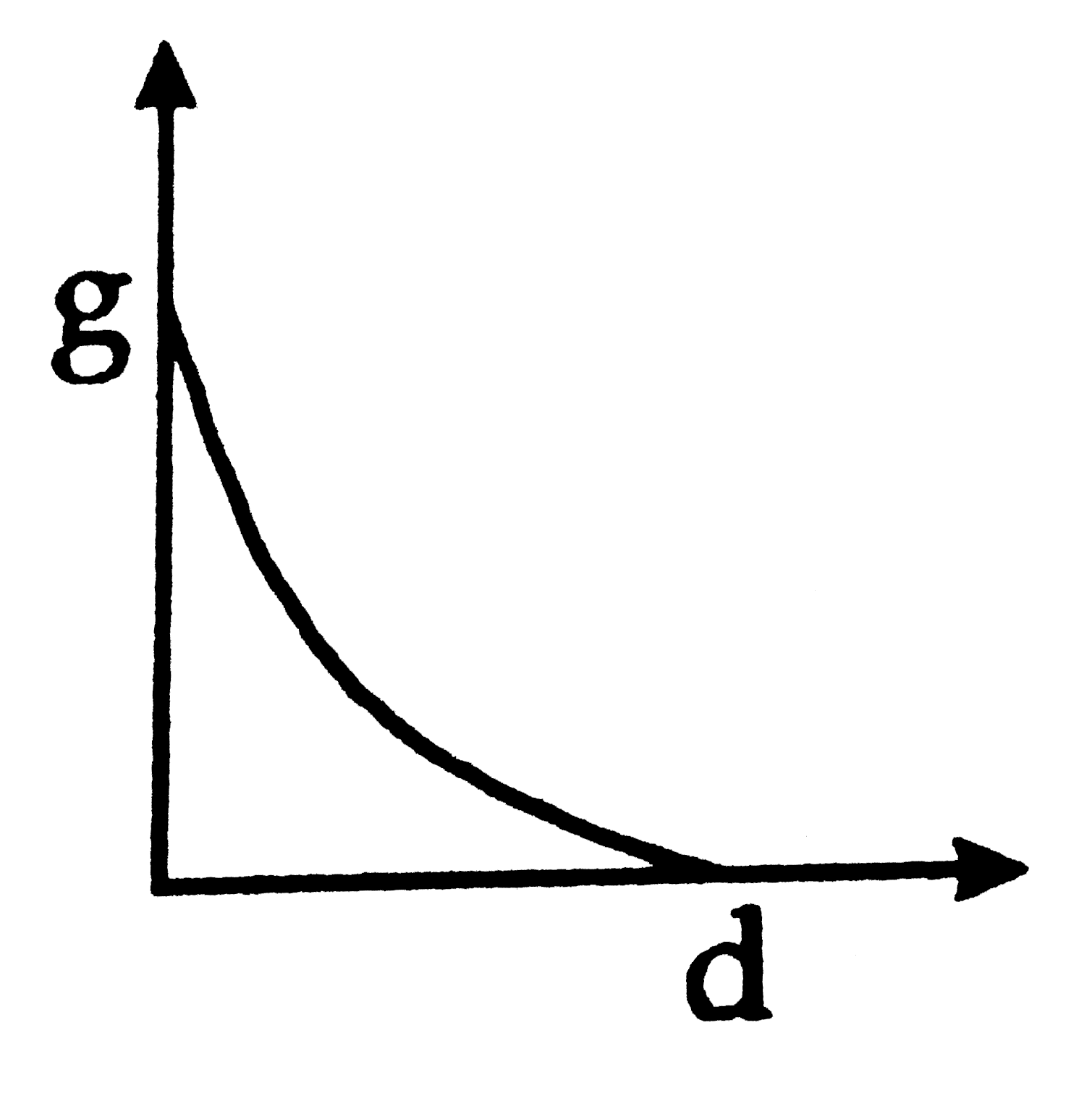 C
C D
D
When the height of a satellite increases from the surface of the earth.
APE decreases,KE increasesBPE decreases,KE decreasesCPE increases,KE decreasesDPE increases,KE increases
Derive an expression for the escape speed of a body from the surface of the Earth. Express it in terms of the mean density of the Earth.
View SolutionDiscuss the variation of g with height and depth.
View SolutionObtain an expression for the acceleration due to gravity on the surface of the earth in terms of mass of the earth and its radius. Discuss the variation of acceleration due to gravity with altitude and depth. If a body is taken to a height R / 4 from the surface of the earth, find percentage decrease in the weight of the body ? Here R is the radius of the earth.
View SolutionDraw graphs showing the variation of accleeration due to gravity with (a) height above the Earth's surface, (b) depth below the Earth's surface.
View SolutionThe orbital velocity of a satellite is given by the expression V=sqrt((GM)/(R + h)), here M is the mass of the Earth, R is the radius of the Earth and 'h' is the height of the satellite from the surface of the Earth. Explain the reasons why the geostationary satellite is not possible to set in orbit around the Earth at two different heights from the surface of the Earth.
View Solution

