A planet of mass M, has two natural satellites with masses m1 and m2. The radii of their circular orbits are $R_{1}$ and $R_{2}$ respectively. Ignore the gravitational force between the satellites. Define $v_{1}, L_{1}, K_{1}$ and $T_{1}$ to be, respectively, the orbital speed, angular momentum, kinetic energy and time period of revolution of satellite 1 , and $v_{2}, L_{2}, K_{2}$ and $T_{2}$ to be he corresponding quantities of satellite 2. Given $m_{1} / m_{2} = 2$ and $R_{1} / R_{2} = 1 / 4$ , match the ratios in List-I to the numbers in List-II.

A

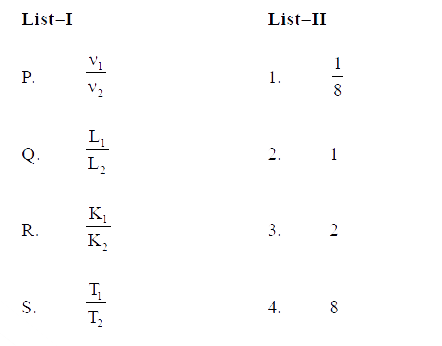
P - 4, Q - 2, R - 1, S - 3

B

P - 3, Q - 2, R - 4, S - 1

C

P - 2, Q - 3, R - 1, S - 4

D

P - 2, Q - 3, R - 4, S - 1

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$P \to v_{0} = \sqrt{\frac{G M}{R}}$
$\frac{v_{1}}{v_{2}} = \sqrt{\frac{R_{2}}{R_{1}}} = \frac{2}{1}$
$Q \to L = m v R$
$\frac{L_{1}}{L_{2}} = \frac{m_{1}}{m_{2}} \times \frac{v_{1}}{v_{2}} \times \frac{R_{1}}{R_{2}} = \frac{2}{1} \times \frac{2}{1} \times \frac{1}{4} = 1$
$R \to K . E . = \frac{G M m}{R}$
$\frac{K_{1}}{K_{2}} = \frac{m_{1}}{m_{2}} \times \frac{R_{2}}{R_{1}} = \frac{2}{1} \times \frac{4}{1} = 8$
$S \to \frac{T_{1}}{T_{2}} = {(\frac{R_{1}}{R_{2}})}^{\frac{3}{2}} = \frac{1}{8}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two satellite fo masses m and 4m orbit the earth in circular orbits of radii 4r and r respectively. The ratio of their orbital speed is
A1
B $\frac{1}{2}$
C $\frac{1}{\sqrt{2}}$
D $\frac{1}{\sqrt{5}}$
Question 2 - Select One
Two satellites of masses 3 m and m orbit the earth in circular orbits of radii r and 3 r respectively. The ratio of the their speeds is
A $1 : 1$
B $\sqrt{3} : 1$
C $3 : 1$
D $9 : 1$
Question 3 - Select One
A binary star system consists of two stars of masses $M_{1}$ and $M_{2}$ revolving in circular orbits of radii $R_{1}$ and $R_{2}$ respectively. If their respective time periods are $T_{1}$ and $T_{2}$ , then
A $T_{1} > T_{2}$ if $R_{1} > R_{2}$
B $T_{1} > T_{2}$ if $M_{1} > M_{2}$
C $T_{1} = T_{2}$
D $\frac{T_{1}}{T_{2}} = {(\frac{R_{1}}{R_{2}})}^{3 / 2}$

MODERN PUBLICATION-GRAVITATION-COMPETITION FILE (Matching Type Questions)

A planet of mass M, has two natural satellites with masses m1 and m2. ...
06:38

Home
Ask Doubt
Profile