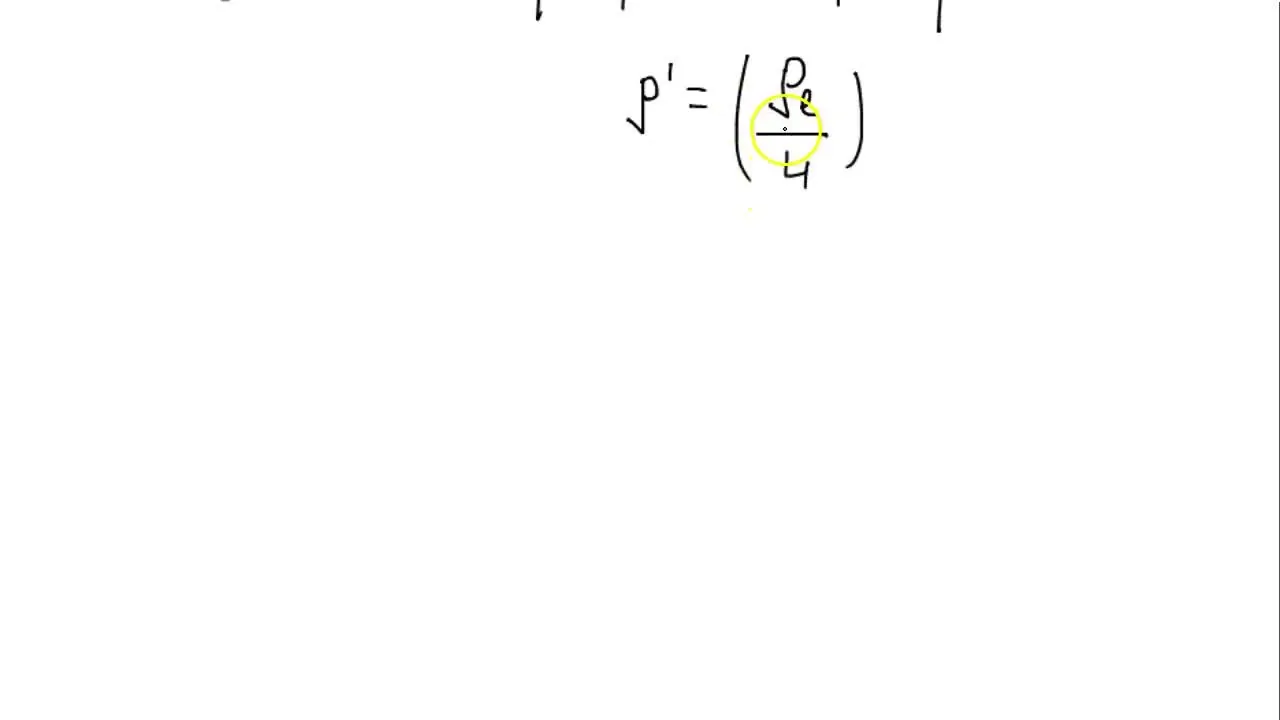Keeping mass unchanged if radius of the earth increases by a factor 4, then by which factor density must have to be changed so that the value of g remains same ?
Decreased to 14th of original density
Related Playlists
- BOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Conceptual Questions19videos
GRAVITATION
- BOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Tough & Tricky Problems10videos
GRAVITATION
- BOOK - MODERN PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Chapter Practice Test15videos
GRAVITATION
- BOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)12videos
MATHEMATICAL TOOLS
Similar Questions
If the radius of the earth be increased by a factor of 5, by what factor its density be changed to keep the value of g of the same?
View SolutionIf the radius of the earth were incresed by a factor of 3, by what factor would its density to be changed to keep 'g' the same ?
View SolutionIf the radius of the earth were increased by a factor of 2 keeping the mass constant, by what factor would its density have to be changed to keep g the same?
View SolutionIf the radius of a cylinder is increased by 25% , by how much per cent the height must be reduced , so that the volume of the cylinder remains the same .
View SolutionIf the radius of the earth decreases by 10%, the mass remaining unchanged, what will happen to the acceleration due to gravity?
View SolutionIf the distance between two masses is increased by a factor of 4, by what factor would the mass of one of them have to be altered to maintain the same gravitational force?
View SolutionIf the distance between two masses is increased by a factor of 5, by what factor would the mass of one of them have to be altered to maintain the same gravitational force? Would this be an increase or decrease in the mass?
View SolutionThe radius of earth is increased by 2%. By what precentage the acceleration due to gravity will change assuming mass remaining unchanged ?
View SolutionThe radius of the earth is reduced by 4%. The mass of the earth remains unchanged. What will be the change in escape velocity?
View SolutionIf the radius of the earth shrinks by 1.5% ( mass remaining same) , then the value of acceleration due to gravity changes by
View Solution