Two sphere AandB of masses m1andm2 respectivelly colides. A is at rest initally and B is moving with velocity v along x-axis. After collision B has a velocity v2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction.
θ=tan−1(−12) to the X - axis
same as that of B
opposite to that of B
θ=tan−1(12) to the X - axis
The correct Answer is:D

Momentum conserved ,along X - direction
m2u1+m1u2=m2(0)+m1v2cosθ
m2v=m1v2cosθ
m2m1v=v2cosθ …(i)
Momentu conerved along Y - direction
0+0=m2v1−m1v2sinθ
m22v=m1v2sinθ
(m2m1v2)=v2sinθ ...(ii)
Divide equation (ii) by (i)
tanθ=12⇒1=tan−1(1/2)
But θ is in anticlockwise direction so takes as negative
Angle =−θ=−tan(12)
tan(−12) (along + X direction )
Topper's Solved these Questions
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (JEE (Main) & Other State Boards for Engineering Entrance)
Explore 31 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (JEE (Advanced) for IIT Entrance)
Explore 7 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (A. Multiple Choice Questions)
Explore 29 Videos
- WAVESBook:MODERN PUBLICATIONChapter:WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
Similar Questions
Two balls A and B of masses 0.3 kg and 0.2 kg respectively are moving along positive X-axis and negaive X-axis with velocities 2.0 m / s. They collide and thereafter move in the directions opposite to their original directions. Find the velocities of A and B after collision. Also, calculate total K.E. of the ball before and after collision.
View SolutionA ball moving with a velocity 12m/s strikes an identical ball at rest.After collision both balls move in directions making 300 with original direction of motion.speeds of the balls after collision are (in ms−1) ?
View Solution
Knowledge Check
Two spheres a and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v/2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction
Asame as that of BBopposite to that of BCθ=tan−1(12) to the x-axisDθ=tan−1(−12) to the x-axisTwo spheres A and B of masses m1andm2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v2direction perpendicular to the original direction. The mass A moves after collision in the direction
Asame as that of BBopposite to that of BCθ=tan−1(12) to the axisDθ=tan−1(−12) to the x-axisA mass m moves with a velocity v and collides inelastically with another identical mass. After collision the 1st mass moves with velocity v√3 in a direction perpendicular to the initial direction of motion. Find the speed of the second mass after collision
AvB√3vC2√3vDv√3
A ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionA sphere of mass m moves with a velocity 2v and collides inelastically with another identical sphere of mass m. After collision the first mass moves with velocity v in a direction perpendicular to the initial direction of motion . Find the speed of the second sphere after collision .
View SolutionA mass ‘m’ moves with a velocity ‘v’ and collides inelastically with another identical mass at rest. After collision the 1st mass moves with velocity v√3 in a direction perpendicular to the initial direction of motion. Find the speed of the 2nd mass after collision :
View SolutionA mass m moves with a velocity v and collides inelastically with another identical mass at rest. After collision, the first mass moves with velocity v√3 in a direction perpendicular to Before collision the initial direction of motion. The speed of the 2nd mass after collision
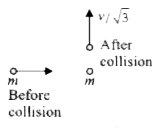
View SolutionA body of mass m moving at a constant velocity v hits another body of the same mass moving with a velocity v/2 but in the opposite direction and sticks to it. The common velocity after collision is
View Solution

