A particle of mass m is moving in a stright line , If x is the distance travelled by the particle then its velocity is given as v = αx , here α is a constant . Calculate work done by all the forces acting on the body when particle is displaced from x = 0 to x = d .
To solve the problem, we will use the work-energy theorem, which states that the net work done on a particle is equal to the change in its kinetic energy. Here are the steps to find the work done by all the forces acting on the particle as it moves from x=0 to x=d.
Step 1: Understand the given information
The velocity v of the particle is given by the equation:
v=αx
where α is a constant and x is the distance travelled by the particle.
Step 2: Express the kinetic energy
The kinetic energy K of a particle of mass m is given by:
K=12mv2
Substituting the expression for v:
K=12m(αx)2=12mα2x2
Step 3: Calculate the initial and final kinetic energy
- Initial kinetic energy Ki when x=0:
Ki=12mα2(0)2=0
- Final kinetic energy Kf when x=d:
Kf=12mα2d2
Step 4: Apply the work-energy theorem
According to the work-energy theorem:
W=Kf−Ki
Substituting the values we found:
W=12mα2d2−0=12mα2d2
Conclusion
The work done by all the forces acting on the particle when it is displaced from x=0 to x=d is:
W=12mα2d2
---
The velocity v of the particle is given by the equation:
v=αx
where α is a constant and x is the distance travelled by the particle.
The kinetic energy K of a particle of mass m is given by:
K=12mv2
Substituting the expression for v:
K=12m(αx)2=12mα2x2
- Initial kinetic energy Ki when x=0:
Ki=12mα2(0)2=0
Kf=12mα2d2
According to the work-energy theorem:
W=Kf−Ki
Substituting the values we found:
W=12mα2d2−0=12mα2d2
The work done by all the forces acting on the particle when it is displaced from x=0 to x=d is:
W=12mα2d2
Topper's Solved these Questions
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Revision Exercise (Very Short Answer Questions)
Explore 31 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Revision Exercise (Additional Questions)
Explore 3 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:NCERT FILE (NCERT Exemplar Problems (Short Answer Type Questions))
Explore 10 Videos
- WAVESBook:MODERN PUBLICATIONChapter:WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
Similar Questions
A particle of mass m moves on a straight line with its velocity varying with the distance travelled according to the equation v=a√x, wher ea is a constant. Find the total work done by all the forces during a displacement from x=0→x=d.
View SolutionThe velocity (v) of a particle of mass m moving along x-axis is given by v=α√x, where α is a constant. Find work done by force acting on particle during its motion from x=0 to x=2m :-
View Solution
Knowledge Check
A particle is moving on X−axis. Its velocity time graph is given in the figure. Find distance travelled by the particle in 5sec.
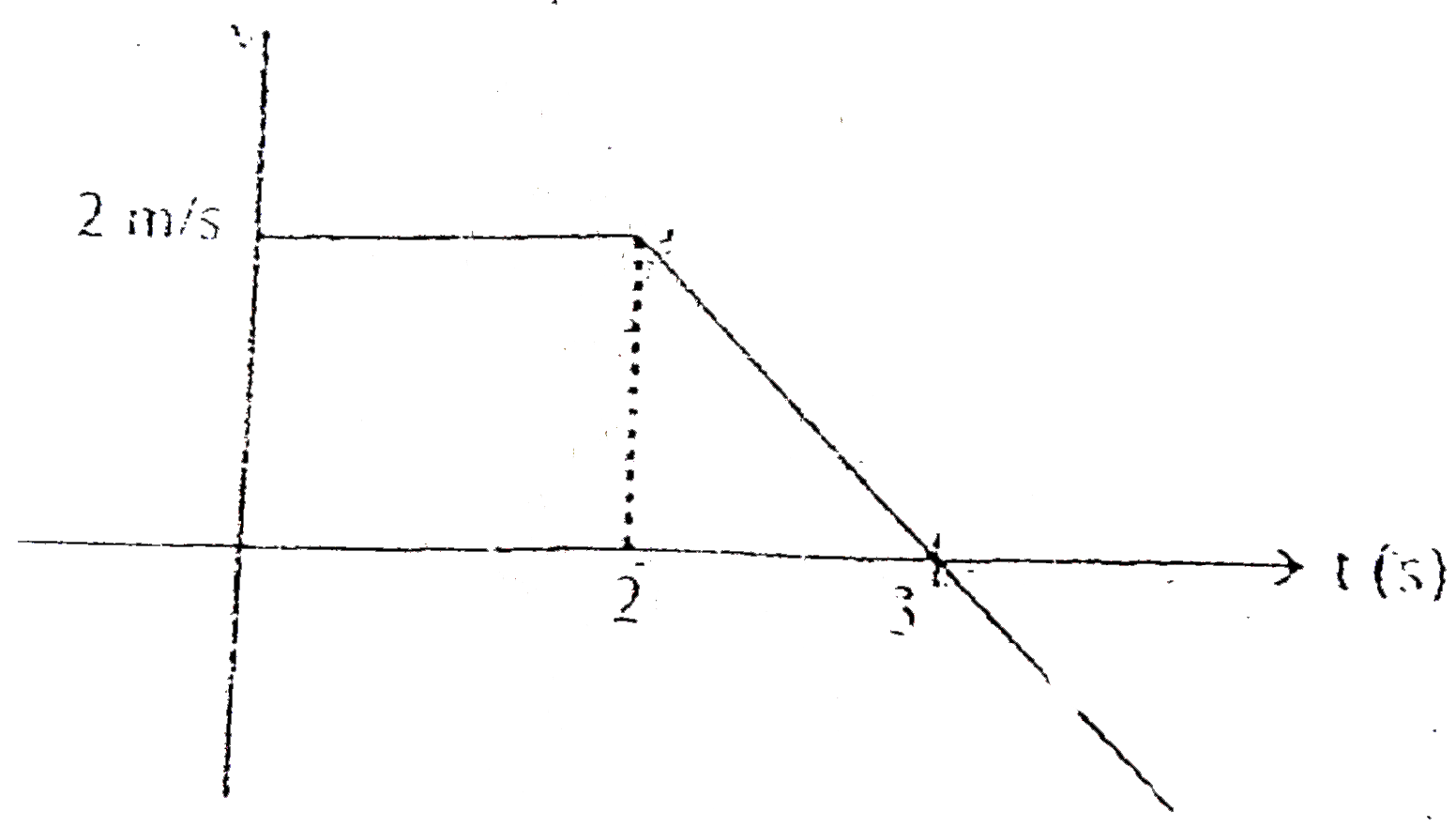 A1mB9mC3mD7m
A1mB9mC3mD7mA particle of mass m initially moving with speed v.A force acts on the particle f=kx where x is the distance travelled by the particle and k is constant. Find the speed of the particle when the work done by the force equals W.
A√km+v2B√2Wm+v2C√2Wk+v2D√W2m+v2A particle of mass m moves with a variable velocity v, which changes with distance covered x along a straight line as v=k√x, where k is a positive constant. The work done by all the forces acting on the particle, during the first t seconds is
A(a) mk4t2B(b) mk4t24C(c) mk4t28D(d) mk4t216
Force acting on a particle varies with x as shown in figure. Calculate the work done by the force as the particle moves from x = 0 to x = 6.0 m.
View SolutionThe velocity (v) of a pariticle of mass m moving along x-axls is given by v=b√x, where b is a constant. Find work done by the force acting on the particle during its motion from x=0 to x=4m.
View SolutionA particle of mass m is moving in the xy-plane such that its velocity at a point (x,y) is given as →v = α(yˆx+2xˆy) where α is a non-zero constant. What is the force →F acting on the particle?
View SolutionA force F = 0.5x + 10 acts on a particle. Here F is in newton and x is in metre. Calculate the work done by the force during the displacement of the particle from x = 0 to x = 2 metre.
View SolutionA particle moves with an initial velocity V0 and retardation αv , where α is a constant and v is the velocity at any time t.
Velocity of particle at time is :
View Solution

