A body undergoing a straight line motion is under the influence of source of constant power. How does its displacement very with time?
To determine how the displacement of a body varies with time when it is under the influence of a constant power, we can follow these steps:
1. Understanding Power:
The power P is defined as the rate at which work is done. Mathematically, it can be expressed as:
P=F⋅v
where F is the force applied and v is the velocity of the body.
2. Relating Power to Mass and Acceleration:
We know that force F can also be expressed using Newton's second law:
F=m⋅a
where m is the mass of the body and a is its acceleration. Since acceleration a can be expressed as dvdt, we can rewrite the power equation as:
P=m⋅a⋅v=m⋅dvdt⋅v
3. Rearranging the Equation:
Rearranging the equation gives us:
P=m⋅v⋅dvdt
We can separate variables to integrate:
Pmdt=vdv
4. Integrating:
Integrating both sides, we have:
∫t0Pmdt=∫vuvdv
This leads to:
Pmt=v22−u22
where u is the initial velocity.
5. Solving for Velocity:
Rearranging the equation to solve for v:
v2=u2+2Ptm
Taking the square root gives us:
v=√u2+2Ptm
6. Finding Displacement:
To find displacement x, we use the relationship:
x−x0=∫t0vdt
Substituting v into the integral:
x−x0=∫t0√u2+2Ptmdt
7. Final Expression for Displacement:
After integrating, we can express the displacement as:
x=x0+m3P((u2+2Ptm)3/2−u3)
Conclusion:
Thus, the displacement of the body varies with time according to the derived equation, showing that it depends on the initial velocity, the constant power, and the mass of the body.
The power P is defined as the rate at which work is done. Mathematically, it can be expressed as:
P=F⋅v
where F is the force applied and v is the velocity of the body.
We know that force F can also be expressed using Newton's second law:
F=m⋅a
where m is the mass of the body and a is its acceleration. Since acceleration a can be expressed as dvdt, we can rewrite the power equation as:
P=m⋅a⋅v=m⋅dvdt⋅v
Rearranging the equation gives us:
P=m⋅v⋅dvdt
We can separate variables to integrate:
Pmdt=vdv
Integrating both sides, we have:
∫t0Pmdt=∫vuvdv
This leads to:
Pmt=v22−u22
where u is the initial velocity.
Rearranging the equation to solve for v:
v2=u2+2Ptm
Taking the square root gives us:
v=√u2+2Ptm
To find displacement x, we use the relationship:
x−x0=∫t0vdt
Substituting v into the integral:
x−x0=∫t0√u2+2Ptmdt
After integrating, we can express the displacement as:
x=x0+m3P((u2+2Ptm)3/2−u3)
Thus, the displacement of the body varies with time according to the derived equation, showing that it depends on the initial velocity, the constant power, and the mass of the body.
Topper's Solved these Questions
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Tough & Tricky (PROBLEMS)
Explore 15 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:NCERT FILE (NCERT Textbook Exercise)
Explore 23 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:PRACTICE PROBLEMS
Explore 27 Videos
- WAVESBook:MODERN PUBLICATIONChapter:WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
Similar Questions
A body is moving undirectionally under the influence of a source of constatn power. It displacement in time t is proportional to (i) t1/2 (ii) t (iii) t3/2 (iv) t2
View SolutionThe velocity of a particle moving in a straight line is directly proportional to 3/4th power of time elapsed. How does its displacement and acceleration depend on time?
View Solution
Knowledge Check
A body is moving unidirectionally under the influence of a sources of constant power. The square of its displacement in time t is proportional to
At3Bt2CtD√tA body is moving unidirectionally under the influence of a source of constant power supplying energy. Which of the diagrams shown in figure. Correctly shows the displacement-time curve for its motion ?
A B
B C
C D
D
A body is moving unidirectionally under the influence of a source of constant power supplying energy. Which of the diagrams shown in figure. Correctly shows the displacement-time curve for its motion ?
A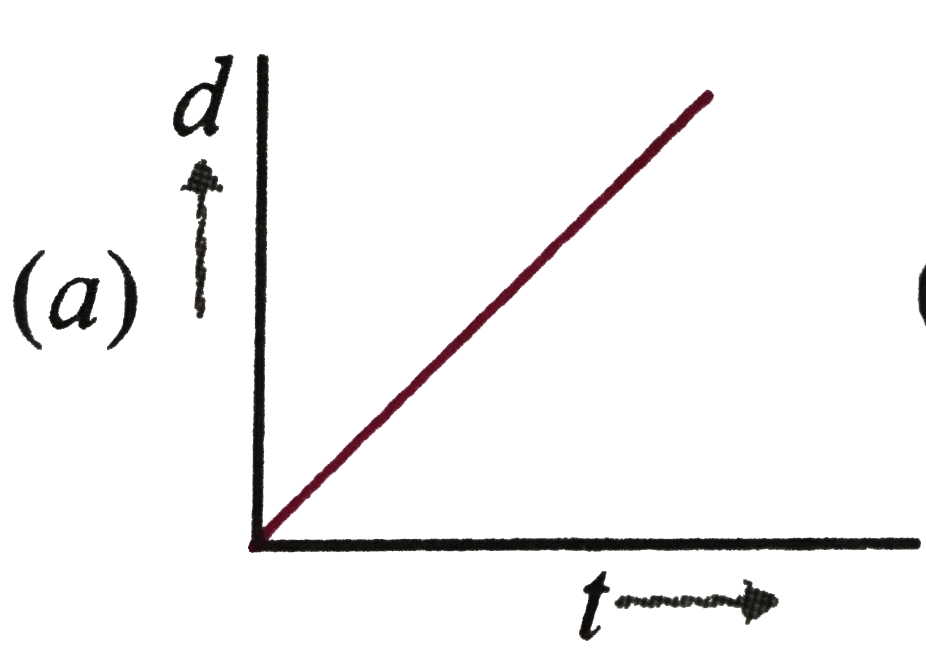 B
B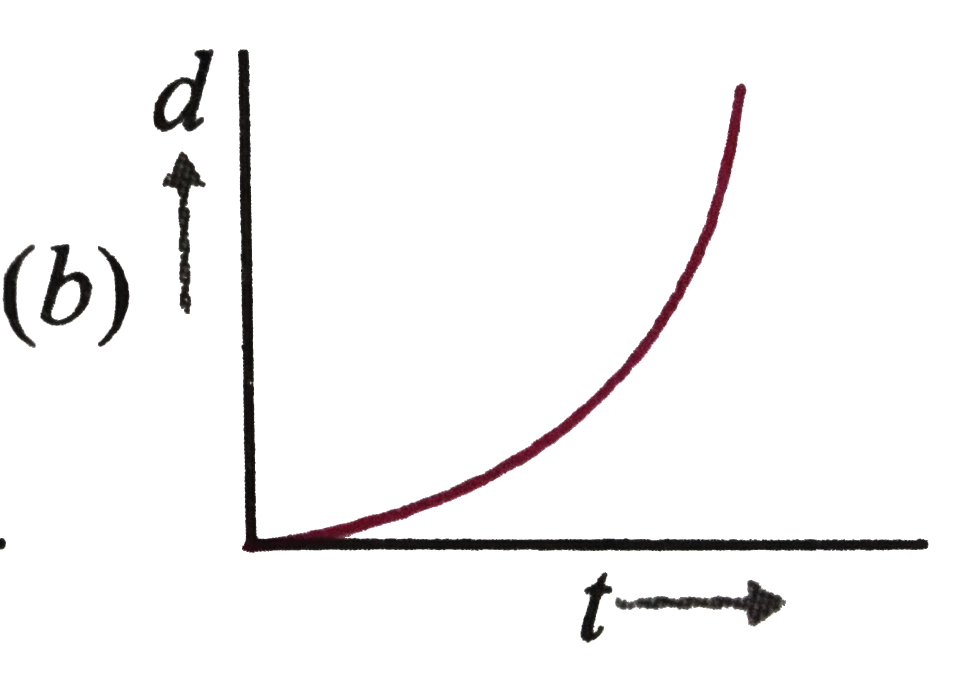 C
C D
D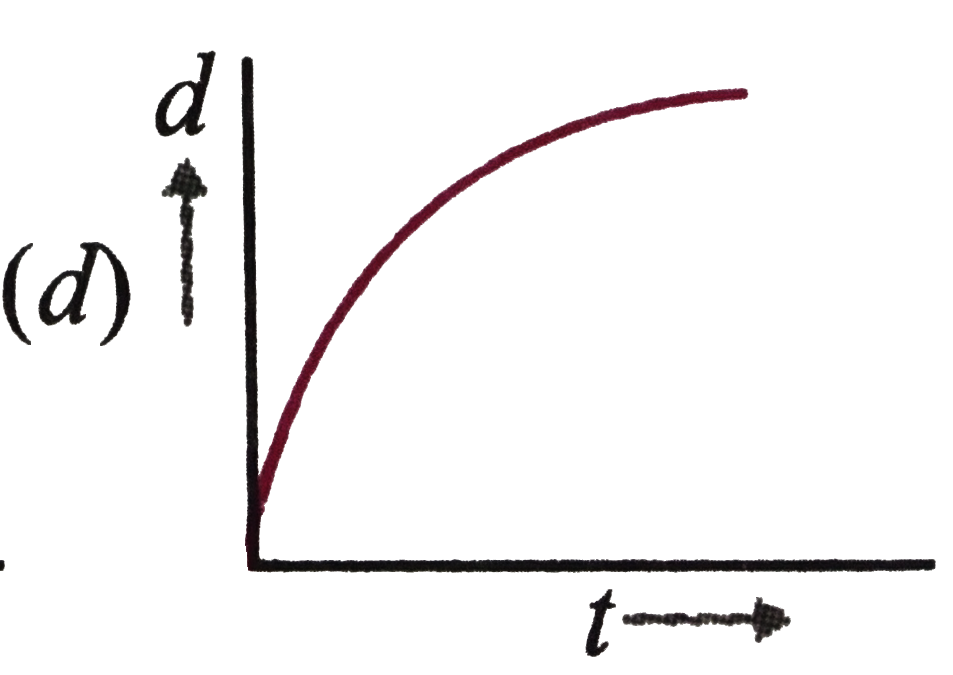
A body is under the influence of a force such that it delivers a constant power p. The variation of position with time of body as
View SolutionA body is moved from rest along a straight line by a machine delivering constant power. The ratio of displacement and velocity (s/v) varies with time t as
View SolutionA body is being moved from rest along a straight line by a machine delivering constant power. The distance covered by body in time t is proportional to
View SolutionA body is moves along a straight line by a machine dellvering a constant power . The distance moved by the body in time t is propertional as
View SolutionA body is moved along a straight line by a machine delivering a constant power. The distance moved by the body in time t is proportional to
View Solution

