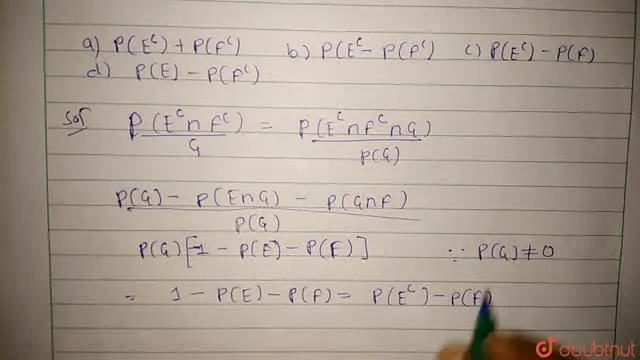Let Ec denote the complement of an event E . Let E,F ,G be pair - wise independent events with P(G)>0andP(EcapF∩G)=0 . Then P(EC∩FC/G) equals : Solution in Kannada
P(EC)+P(FC)
P(EC−P(FC)
P(EC)−P(F)
P(E)−P(FC)
The correct Answer is:C
Step by step video, text & image solution for Let E^(c ) denote the complement of an event E . Let E,F ,G be pair - wise independent events with P(G) gt 0 and P(E ca p F cap G) = 0 . Then P(E^(C )cap F^(C )//G) equals : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - LATEST QUESTIONS FROM AIEEE/JEE EXAMINATIONS13videos
PROBABILITY
- BOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - RECENT COMPETITIVE QUESTIONS (QUESTIONS FROM KARNATAKA CET & COMED )11videos
PROBABILITY
- BOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - RECENT COMPETITIVE QUESTIONS (QUESTIONS FROM KARNATAKA CET & COMED )11videos
PROBABILITY
- BOOK - MODERN PUBLICATIONCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Recent Competitive Questions6videos
PERMUTATIONS AND COMBINATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - QUADRATIC EQUATIONS EXERCISE - LATEST QUESTIONS FROM AIEEE/JEE EXAMINATIONS13videos
QUADRATIC EQUATIONS
Similar Questions
An urn contains nine balls of which three are red , four are blue and two are green . Three balls are drawn at random without replacement from the urn . The probability that the three balls have different colours is :
03:21View SolutionA and B are two such that P(A)≠0,P(B/A) if : (i) A is subset of B (ii) A∩B=ϕ are respectivey :
02:59View SolutionA and B are two such that P(A)≠0,P(B/A) if : (i) A is subset of B (ii) A∩B=ϕ are respectivey :
02:25View SolutionHow many 5 digit telephone numbers can be constructed using the digits 0 to 9, if each number starts with 67 and no digit appears more than once ?
02:00View SolutionLet p and q be real numbers such that p ≠ 0 , p3≠ q and p3≠−q. if αandβ are non-zero complex numbers satisfying α+β=−p and α3+β3=q,
then a quadratic equation having αβandβα as its roots is :12:56View SolutionLet Ec denote the complement of an event E. Let E,F,G be pairwise independent events with P(G)>0 and P(E∩F∩G)=0 Then P(Ec∩Fc∩G) equals (A) P(Ec)+P(Fc) (B) P(Ec)−P(Fc) (C) P(Ec)−P(F) (D) P(E)−P(Fc)
02:29View SolutionLet E∘ denotes the complement of an event E. If E, F, G are pairwise independent events with P(G)>0 and P(E∩F∩G)=0. Then, P(E∘∩F∘∣G) equals :
09:12View SolutionIf E and F are events with P(E)≤P(F)andP(E∩F)>0, then :
05:57View SolutionIf E and F are events with P(E)≤P(F)andP(E∩F)>0 then :
View SolutionA fair die is rolled. Consider events E = {1,3,5}, F = {2,3} and G = {2,3,4,5} Find
(i) P(E|F) and P(F|E) (ii) P(E|G) and P(G|E)
(iii) P((E∪F)∣G) and P((E∩F)∣G)02:40View SolutionA fair die is rolled . Consider events E = {1, 3, 5} F = {2, 3} and G = {2, 3, 4, 5} . Find
P(E/F)andP(F/E)04:43View SolutionA fair die is rolled. Consider events E = {1,3,5}, F = {2,3} and G = {2,3,4,5} Find
(i) P(E|F) and P(F|E) (ii) P(E|G) and P(G|E)
(iii) P((E∪F)∣G) and P((E∩F)∣G)03:42View SolutionA fair die is rolled. Consider events E = {1,3,5}, F = {2,3} and G = {2,3,4,5} Find
(i) P(E|F) and P(F|E) (ii) P(E|G) and P(G|E)
(iii) P((E∪F)∣G) and P((E∩F)∣G)02:38View Solutionयदि E और F ऐसी घटनायें हैं जिनके लिये P(E)≤P(F) और P(E∩F)>0 हो, तो
02:32View SolutionIf E and F are independent events such that 0<P(E)<1 and 0<P(F)<1, then (a) EandF are mutually exclusive (b) EandFc (the complement of the event F ) are independent (c) EcandFc are independent (d) P(E/F)+P(Ec/F)=1
03:08View Solution