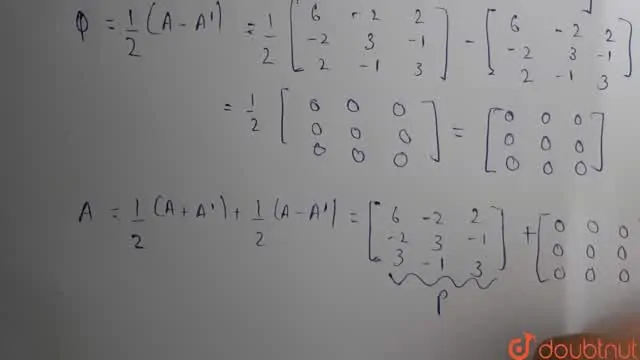Express the following as the sum of symmetric and skew - symmetric matrices :
⎡⎢⎣6−22−23−12−13⎤⎥⎦
The correct Answer is:⎡⎢⎣6−22−23−12−13⎤⎥⎦+⎡⎢⎣000000000⎤⎥⎦
Step by step video, text & image solution for Express the following as the sum of symmetric and skew - symmetric matrices : [(6,-2,2),(-2,3,-1),(2,-1,3)] by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - MODERN PUBLICATIONCHAPTER - MATRICESEXERCISE - Exercise 3 (f) Short Answer Type Questions15videos
MATRICES
- BOOK - MODERN PUBLICATIONCHAPTER - MATRICESEXERCISE - Exercise 3 (f) Long Answer Type Questions (I)10videos
MATRICES
- BOOK - MODERN PUBLICATIONCHAPTER - MATRICESEXERCISE - Exercise 3 (e ) Long Answer Type Questions (I)27videos
MATRICES
- BOOK - MODERN PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - Chapter Test12videos
LINEAR PROGRAMMING
- BOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - MOCK TEST SECTION D6videos
PROBABILITY
Similar Questions
Express the following as the sum of symmetric and skew - symmetric matrices :
⎡⎢⎣323453245⎤⎥⎦View SolutionExpress the following as the sum of symmetric and skew - symmetric matrices :
⎡⎢⎣33−10−21−4−52⎤⎥⎦View SolutionExpress the following as the sum of symmetric and skew - symmetric matrices :
⎡⎢⎣123345567⎤⎥⎦View SolutionExpress the following as the sum of symmetric and skew - symmetric matrices :
⎡⎢⎣1311325−45⎤⎥⎦View SolutionExpress the following as the sum of symmetric and skew - symmetric matrices :
⎡⎢⎣2−4518−2739⎤⎥⎦View SolutionExpress the following as the sum of symmetric and skew - symmetric matrices :
⎡⎢⎣25−1315769⎤⎥⎦View SolutionExpress the following as the sum of symmetric and skew - symmetric matrices :
⎡⎢⎣12−3705−489⎤⎥⎦View SolutionExpress matrices as the sum of a symmetric and skew symmetric matrix ⎡⎢⎣6−22−23−12−13⎤⎥⎦
View SolutionExpress the following matrilx as the sum of a symmetric and skey symmetric matrix ⎡⎢⎣124681357⎤⎥⎦
View SolutionExpress [3−41−1] as the sum of symmetric and skew-symmetric matrices.
View Solution