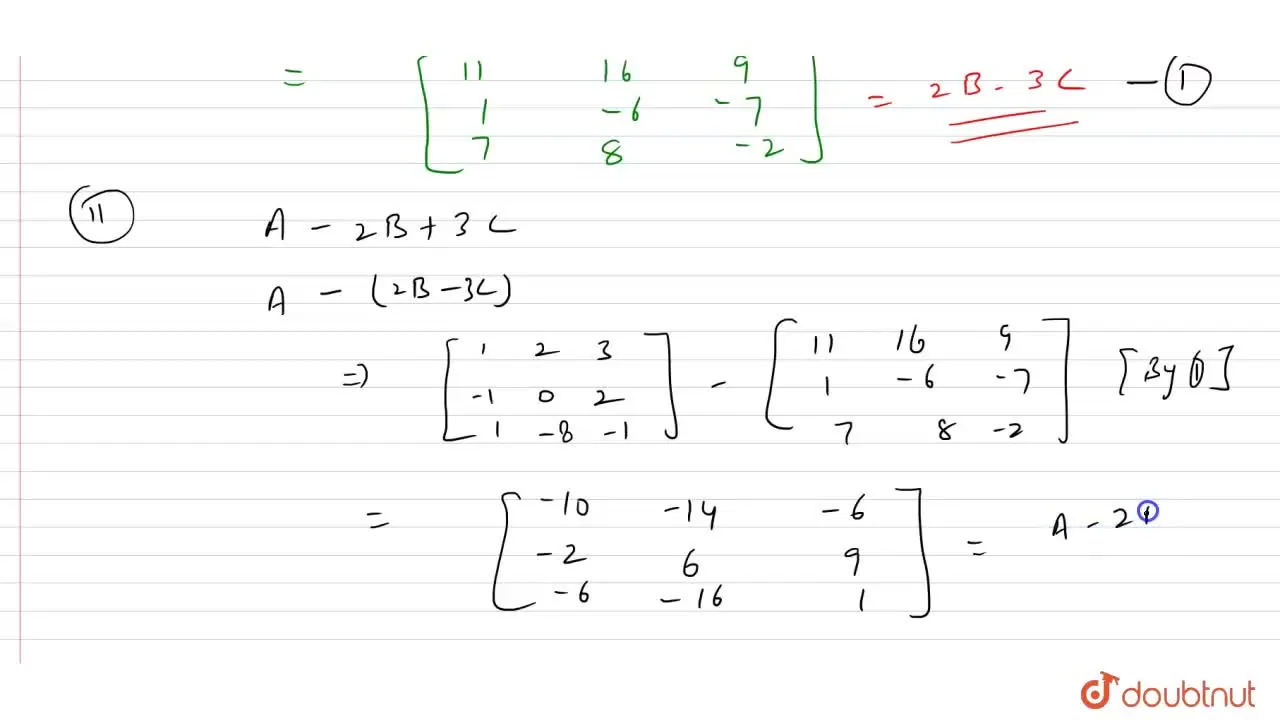If A=⎡⎢⎣123−1021−8−1⎤⎥⎦,B=⎡⎢⎣456−101212⎤⎥⎦,C=⎡⎢⎣−1−21−123−1−22⎤⎥⎦, find (i) 2B−3C (ii) A−2B+3C.
The correct Answer is:(i) ⎡⎢⎣111691−6−778−2⎤⎥⎦ (ii) ⎡⎢⎣−10−14−6−269−6−161⎤⎥⎦
Step by step video, text & image solution for If A=[(1,2,3),(-1,0,2),(1,-8,-1)],B=[(4,5,6),(-1,0,1),(2,1,2)],C=[(-1,-2,1),(-1,2,3),(-1,-2,2)], find (i) 2B-3C (ii) A-2B+3C. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - MODERN PUBLICATIONCHAPTER - MATRICESEXERCISE - Exercise 3 (d ) Short Answer Type Questions20videos
MATRICES
- BOOK - MODERN PUBLICATIONCHAPTER - MATRICESEXERCISE - Exercise 3 (d) Long Answer Type Questions I28videos
MATRICES
- BOOK - MODERN PUBLICATIONCHAPTER - MATRICESEXERCISE - Exercise 3 (c ) Short Answer Type Questions11videos
MATRICES
- BOOK - MODERN PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - Chapter Test12videos
LINEAR PROGRAMMING
- BOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - MOCK TEST SECTION D6videos
PROBABILITY
Similar Questions
If A=⎡⎢⎣123−1021−31⎤⎥⎦,B=⎡⎢⎣456−101212⎤⎥⎦,C=⎡⎢⎣−1−21−123−1−22⎤⎥⎦ find A-2B+3C. Also verify that (A+B)+C=A+(B+C).
View SolutionIf A=⎡⎢⎣123−1021−3−⎤⎥⎦,B=⎡⎢⎣456−101212⎤⎥⎦andC=⎡⎢⎣−1−21−123−1−22⎤⎥⎦ verify that A+(B+C)=(A+B)+C
View SolutionIf A=⎡⎢⎣123−1021−3−1⎤⎥⎦, B= ⎡⎢⎣456−101212⎤⎥⎦andC=⎡⎢⎣−1−21−123−1−22⎤⎥⎦ verify that A(B+C)=AB+AC.
View SolutionIf A=⎡⎢⎣123−102−2−31⎤⎥⎦,B=⎡⎢⎣451−103212⎤⎥⎦,C=⎡⎢⎣−1−21−123−1−22⎤⎥⎦ then A−2B+3C=
View SolutionIf A=[234−302],B=[3−4−5121],C=[5−10703], then find A+B+C.
View SolutionifA=⎡⎢⎣3211233−61⎤⎥⎦,B=⎡⎢⎣1402−30120⎤⎥⎦
andC=⎡⎢⎣123321879⎤⎥⎦,then find AB-AC.View SolutionIf A=[2−142],B=[43−21],C=[−2−3−1−2], find the value of A+B+C.
View SolutionifA=⎡⎢⎣12−35021−11⎤⎥⎦,B=⎡⎢⎣3−12425203⎤⎥⎦andc=⎡⎢⎣4120321−23⎤⎥⎦, then compure (A+B) and (B-C), Also , verify that A+(B-C)=(A+B)-C.
View SolutionIf A=[123231] and B=[3−13−102], then find 2A−B.
View SolutionIf A=[−102314],B=[0−251−31]andC=[1−5260−4], then find (2A−3B+4C).
View Solution