A long wire carrying a steady current I lies in the plane of circular conducting loop placed at a certain distance from the wire. There will be an induced current in the loop if it is
moved parallel to the wire
roatated about an axis perpendicular to the plane of the loop passing through the centre of the loop
rotated about an axis parallel to the wire passing through the centre of the loop
moved away from the wire
The correct Answer is:C, D
To determine when there will be an induced current in a circular conducting loop placed at a certain distance from a long wire carrying a steady current I, we can analyze the situation based on the principles of electromagnetic induction.
1. Understanding the Setup:
- We have a long wire carrying a steady current I.
- A circular conducting loop is placed at a distance r from the wire.
- The magnetic field B created by the long wire at a distance r is given by Ampere's Law:
B=μ0I2πr
- Here, μ0 is the permeability of free space.
2. Induced Current Condition:
- According to Faraday's Law of Electromagnetic Induction, an induced current will occur in the loop if there is a change in magnetic flux Φ through the loop over time.
- The magnetic flux Φ through the loop is given by:
Φ=B⋅A
- Where A is the area of the loop.
3. Analyzing Different Scenarios:
- Option 1: Move Parallel to the Wire:
- If the loop is moved parallel to the wire, the distance r remains constant.
- Since B is constant, the magnetic flux Φ remains constant.
- Therefore, there is no change in flux, and the induced current is zero.
- Option 2: Rotate about an Axis Perpendicular to the Plane of the Loop:
- Rotating the loop about an axis perpendicular to its plane does not change the area A or the magnetic field B.
- Thus, the magnetic flux Φ remains constant, leading to zero induced current.
- Option 3: Rotate about an Axis Parallel to the Wire:
- If the loop is rotated about an axis parallel to the wire, the area A of the loop changes.
- This change in area leads to a change in magnetic flux Φ.
- Therefore, an induced current will be generated in this scenario.
- Option 4: Move Away from the Wire:
- As the loop moves away from the wire, the distance r increases.
- This results in a decrease in the magnetic field B (since B is inversely proportional to r).
- Consequently, the magnetic flux Φ changes, leading to an induced current.
4. Conclusion:
- Induced current occurs in the following scenarios:
- When the loop is rotated about an axis parallel to the wire (Option 3).
- When the loop is moved away from the wire (Option 4).
- Therefore, Options 3 and 4 are correct.
- We have a long wire carrying a steady current I.
- A circular conducting loop is placed at a distance r from the wire.
- The magnetic field B created by the long wire at a distance r is given by Ampere's Law:
B=μ0I2πr
- Here, μ0 is the permeability of free space.
- According to Faraday's Law of Electromagnetic Induction, an induced current will occur in the loop if there is a change in magnetic flux Φ through the loop over time.
- The magnetic flux Φ through the loop is given by:
Φ=B⋅A
- Where A is the area of the loop.
- Option 1: Move Parallel to the Wire:
- If the loop is moved parallel to the wire, the distance r remains constant.
- Since B is constant, the magnetic flux Φ remains constant.
- Therefore, there is no change in flux, and the induced current is zero.
- Rotating the loop about an axis perpendicular to its plane does not change the area A or the magnetic field B.
- Thus, the magnetic flux Φ remains constant, leading to zero induced current.
- If the loop is rotated about an axis parallel to the wire, the area A of the loop changes.
- This change in area leads to a change in magnetic flux Φ.
- Therefore, an induced current will be generated in this scenario.
- As the loop moves away from the wire, the distance r increases.
- This results in a decrease in the magnetic field B (since B is inversely proportional to r).
- Consequently, the magnetic flux Φ changes, leading to an induced current.
- Induced current occurs in the following scenarios:
- When the loop is rotated about an axis parallel to the wire (Option 3).
- When the loop is moved away from the wire (Option 4).
- Therefore, Options 3 and 4 are correct.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:FIITJEEChapter:ELECTROMAGNETIC INDUCTIONExercise:COMPREHENSIONS - I
Explore 5 Videos
- ELECTROMAGNETIC INDUCTIONBook:FIITJEEChapter:ELECTROMAGNETIC INDUCTIONExercise:COMPREHENSIONS - II
Explore 3 Videos
- ELECTROMAGNETIC INDUCTIONBook:FIITJEEChapter:ELECTROMAGNETIC INDUCTIONExercise:ASSIGNMENT PROBLEMS (ASSERTION REASONING TYPE)
Explore 2 Videos
- ELASTICITY AND WAVES Book:FIITJEEChapter:ELASTICITY AND WAVES Exercise:Assignment Problems (Objective) Level-II
Explore 15 Videos
- ELECTROMAGNETIC INDUCTION AND AC CURRENTBook:FIITJEEChapter:ELECTROMAGNETIC INDUCTION AND AC CURRENTExercise:Example
Explore 15 Videos
Similar Questions
A long straight current carrying wire passes normally through the centre of circular loop. If the current through the wire increases, will there be an induced emf in the loop ? Justify.
View SolutionA long straight current carrying wire passes normally through the centre of circular loop. If the current through the wire increases, will there be an induced emf in the loop ? Justify.
View Solution
Knowledge Check
A wire loop carrying current I is placed in the x-y plane as shown. Magnetic induction at P is
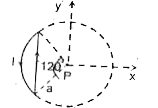 Aμ0I2a(√3π−13)Bμ0I2a(13−π√3)Cμ0I2a(13+√3π)Dμ0I2a(√3π−13)
Aμ0I2a(√3π−13)Bμ0I2a(13−π√3)Cμ0I2a(13+√3π)Dμ0I2a(√3π−13)A long straight wire carrying current I and a square conducting wire loop of side l , at a distance 'a' from current wire as shown in the figure. Both the current wire and loop are in the plane of paper. Find the magnetic flux of current wire, passing through the loop.
Aμ02π.Illoge.a+IaBμ04π.Illoge.a+IaCμ02π.IlDμ04π.IA long wire carrying a steady current is bent into a circular loop of one turn. The magnetic field at the centre of the loop is B. It is then bent into a circular coil of n turns. The magnetic field at the centre of this coil of n turns will be
AnBBn2BC2nBD2n2B
Consider a long infinite wire carrying a time varying current i=kt(k>0). A circular loop of radius a and resistance R is placed with its centre at a distance d from the wire (a<<d). Find out the induced current in the loop?
View SolutionA long straight current carrying wire passes normally through the centre of circular loop. If the current through the wire increases, will there be an induced emg in the loop ? Justify.
View SolutionAn electron moves along the line AB with constant velocity V which lies in the same plane as a circular loop of conducting wire , as shown in the figure . What will be the direction of current induced in the loop ?
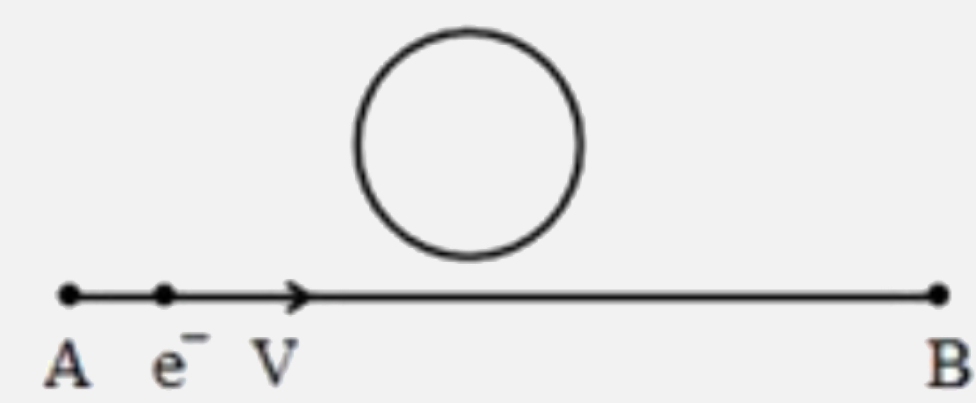
View SolutionAn electron moves along the line AB with constant velocity V which lies in the same plane as a circular loop of conducting wire , as shown in the figure . What will be the direction of current induced in the loop ?

View SolutionTwo different wire loops are concentric and lie in the same plane. The current in the outer loop is clockwise and increasing with time. The induced current in the inner loop then is
View Solution

