For the situation described in figure, the magnetic field changes with time according to
B=(2.00t3−4.00t2+0.8)t and r2=2R=5.0cm

(a) Calculate the force on an electron located at P2 at t=2.00s
(b) What are the magnitude and direction of the electric field at P1 when t=3.00s and r1=0.02m.
8×10−2 N (downward and to the rigth perpendicular to r2 )
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:FIITJEEChapter:ELECTROMAGNETIC INDUCTIONExercise:ASSIGNMENT PROBLEMS ( SUBJECTIVE ) Level -I True and False
Explore 5 Videos
- ELECTROMAGNETIC INDUCTIONBook:FIITJEEChapter:ELECTROMAGNETIC INDUCTIONExercise:ASSIGNMENT PROBLEMS ( SUBJECTIVE ) LEVEL - II & III
Explore 15 Videos
- ELECTROMAGNETIC INDUCTIONBook:FIITJEEChapter:ELECTROMAGNETIC INDUCTIONExercise:ASSIGNMENT PROBLEMS ( SUBJECTIVE ) Level -I
Explore 5 Videos
- ELASTICITY AND WAVES Book:FIITJEEChapter:ELASTICITY AND WAVES Exercise:Assignment Problems (Objective) Level-II
Explore 15 Videos
- ELECTROMAGNETIC INDUCTION AND AC CURRENTBook:FIITJEEChapter:ELECTROMAGNETIC INDUCTION AND AC CURRENTExercise:Example
Explore 15 Videos
Similar Questions
A magentic field directed into the page changes with time according to B=(0.0300t2+1.4.40)T, where t is in seconds. The field has a circular cross section of radius R=2.50cm. What are the magitude and direction of the electric field at point P1 when t=3.00s and r1=0.0200m?

View SolutionThe electric potential at points in an xy plane is given by V=(2.00V/m2)x2−(3.00V/m2)y2. What are (a) the magnitude and (b) angle (relative to +x) of the electric field at the point (4.00 m, 2.00 m)?
View Solution
Knowledge Check
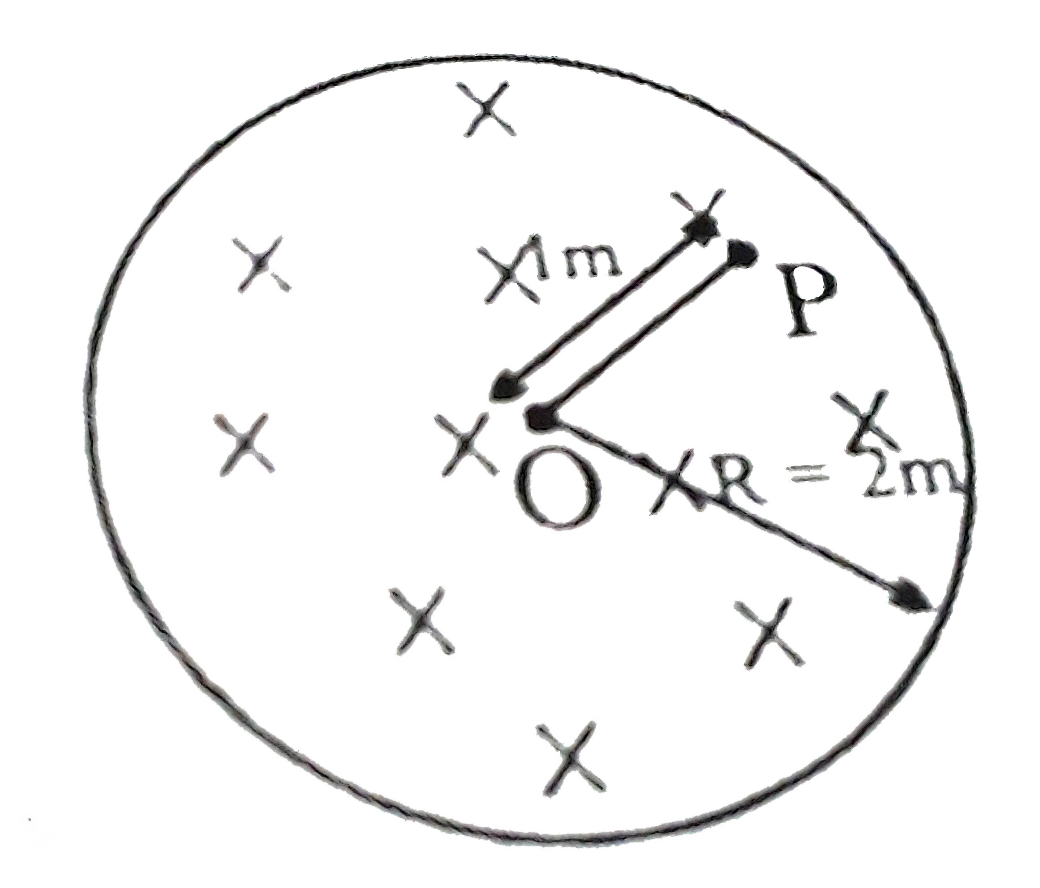
A uniform but time varying magnetic field B=(2t3+24t)T is present in a cylindrical region of radius R=2.5 cm as shown in figure.

The force on an electron at P at t=2.0 s isA96×10−21NB48x10−21NC24×10−21NDzeroThe magnetic field in a certain cylindrical region is changing with time according to the law B=[16−4t2] Tesla . The magnitude of induced electric field at point P at time t= time =2 sec , is
 A8 volt/mB6 volt/mC4 volt/mDnone
A8 volt/mB6 volt/mC4 volt/mDnoneIn a cylinder region of radius R, a uniform magnetic field is there which is increasing with time, according as B=B0t2. A positive point charge q is released from rest at P(OP=R2) at t=0 [the instant the field is switched on]
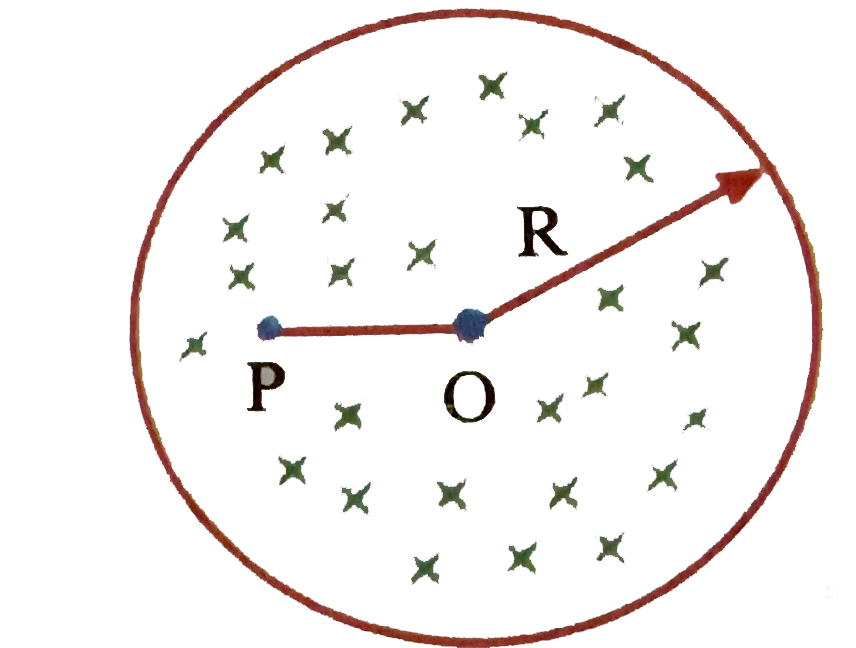
The force experienced by, the point charge at t=1s, is (R=2m)AqB0, anti-clockwiseBqB0, clockwiseC2qB0, anti-clockwiseD2qB0, clockwise
The position of a particle is given by →r=3.0t→i+2.0t2ˆj+5.0ˆk
Where is in seconds and the coefficients have the proper unit for r to be in maters . (a) Find v(t) and a(t) of the particle .
(b) Find the magnitude and direction of v(t)att=1.0s
View SolutionA small circular loop of area 2.00 cm2 is placed in the plane of, and concentric with, a large circular loop of radius 1.00 m. The current in the large loop is changed at a constant rate from 50.0 A to -50.0 A (a change in direction) in a time of 1.00 s, starting at t= 0. What is the magnitude of the magnetic field B at the center of the small loop due to the current in the large loop at (a) t = 0, (b) t = 0.500 s, and ( c) t = 1.00 s? ( d) From t= 0 to t= 1.00 s, is →B reversed? Because the inner loop is small, assume →B is uniform over its area. (e) What emf is induced in the small loop at t = 0.500 s?
View SolutionA 0.25 kg puck is initially stationary on an ice surface with negligible friction. At time t = 0, a horizontal force begins to move the puck. The force is given by →F=(12.0−3.00t2)ˆi, with →F in newtons and t in seconds, and it acts until its magnitude is zero. (a) What is the magnitude of the impulse on the puck from the force between t= 0.750 s and t = 1.25 s? (b) What is the change in momentum of the puck between t=0 and the instant at which F=0?
View SolutionA uniform but time varying magnetic field B=(2t3+24t)T is present in a cylindrical region of radius R=2.5cm as shown in figure.

In the previous problem, the direction of circular electric lines at t=1s is
View SolutionA stationary circular loop of radius a is located in a magnetic field which varies with time from t=0→t=T according to law B=B0t(T−t). If plane of loop is normal to the direction of field and resistance of the loop is R, calculate
amount of heat generated in the loop during this interval.
View Solution

