The current through an inductor of 1H is given by i=31sint. Find the voltage across the inductor.
The correct Answer is:3(tcost+sint)
Step by step video, text & image solution for The current through an inductor of 1H is given by i =31 sin t. Find the voltage across the inductor. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:FIITJEEChapter:ELECTROMAGNETIC INDUCTIONExercise:ASSIGNMENT PROBLEMS ( SUBJECTIVE ) Level -I Fill in the blank
Explore 5 Videos
- ELECTROMAGNETIC INDUCTIONBook:FIITJEEChapter:ELECTROMAGNETIC INDUCTIONExercise:ASSIGNMENT PROBLEMS ( SUBJECTIVE ) Level -I True and False
Explore 5 Videos
- ELECTROMAGNETIC INDUCTIONBook:FIITJEEChapter:ELECTROMAGNETIC INDUCTIONExercise:Matrix Match Type
Explore 12 Videos
- ELASTICITY AND WAVES Book:FIITJEEChapter:ELASTICITY AND WAVES Exercise:Assignment Problems (Objective) Level-II
Explore 15 Videos
- ELECTROMAGNETIC INDUCTION AND AC CURRENTBook:FIITJEEChapter:ELECTROMAGNETIC INDUCTION AND AC CURRENTExercise:Example
Explore 15 Videos
Similar Questions
Knowledge Check
If the current through an inductor of 2 H is given by I=tsintA, then the voltage across the inductor is
Acost+tsintB2tcost+2sintCtcost+sintD2tsint+2costEnergy can be stored by an LC circuit oscillating at its natural frequency. Energy stored in a capacitor is in form of electric field between the plates. An inductor stores energy in form of magnetic field. If the inductor connected across capacitor, the voltage across the capacitor will drive the current through inductor, building up a magnetic field around it. The voltage across the capacitor falls to zero as the charge is used up by the current flow. Now the energy stored in the coil's magnetic field induces a voltage across the coil, because inductor opposes the current change. Thus energy required to charge the capacitor is extracted from the magnetic field.
If we increase the value or L four times in LC oscillator, the frequency of oscillation is:AIncreased 4 timesBDecreased 4 timesCIncreased 2 timesDDecreased 2 timesEnergy can be stored by an LC circuit oscillating at its natural frequency. Energy stored in a capacitor is in form of electric field between the plates. An inductor stores energy in form of magnetic field. If the inductor connected across capacitor, the voltage across the capacitor will drive the current through inductor, building up a magnetic field around it. The voltage across the capacitor falls to zero as the charge is used up by the current flow. Now the energy stored in the coil's magnetic field induces a voltage across the coil, because inductor opposes the current change. Thus energy required to charge the capacitor is extracted from the magnetic field.

We cannot use LC oscillator:to, produce:AVery high frequenciesBVery low.frequenciesCHigh frequenciesDAudio frequencies
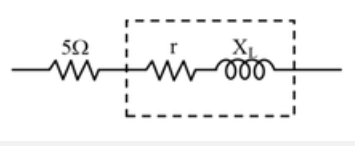
The current through an inductor of impedance 10Ω lags behind the voltage by a phase of 60∘ when just the inductor is connected to the ac source. Now the inductor is connected to a 5Ω resistance in series, then the net impedance of the circuit is
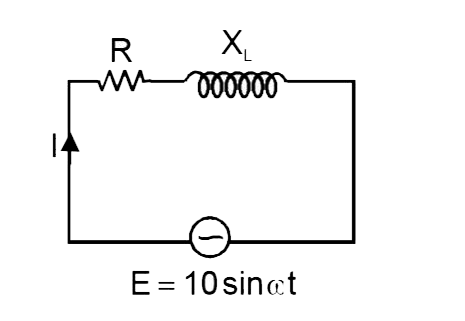
View SolutionAn ac-generator supplying voltage E to a circuit which consists of a resistor of resistance 3Ω and an inductor of reactance 4Ω as shown in the figure. The voltage across the inductor at t=π/ω is
View SolutionEnergy can be stored by an LC circuit oscillating at its natural frequency. Energy stored in a capacitor is in form of electric field between the plates. An inductor stores energy in form of magnetic field. If the inductor connected across capacitor, the voltage across the capacitor will drive the current through inductor, building up a magnetic field around it. The voltage across the capacitor falls to zero as the charge is used up by the current flow. Now the energy stored in the coil's magnetic field induces a voltage across the coil, because inductor opposes the current change. Thus energy required to charge the capacitor is extracted from the magnetic field.

For LC oscillator, the frequency of oscillator is:
View SolutionThe current in ampere through an inductor is
i(10+20t)
Here t is in second. The induced emf in the inductor 4V.
Total flux linked with the inductor at t= 2 is
View SolutionThe current in ampere through an inductor is
i(10+20t)
Here t is in second. The induced emf in the inductor 4V.
The self inductance of the indicator is, L…..H,
View Solution

