A particle moves according to the law given below where x, v and a are displacement,velocity and acceleration respectively and ω, A are + ve constant then match the following.

A→(p,q,r,s),(B)→(r,s),(C)→(p,q,r,s),(D)→(p,q,r,s)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Exercise
Explore 28 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Subjective) (Level)
Explore 20 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Numerical Based Questions
Explore 6 Videos
- SEMICONDUCTOR AND DEVICEBook:FIITJEEChapter:SEMICONDUCTOR AND DEVICEExercise:SOLVED PROBLEMS Objective: Level-I
Explore 20 Videos
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
Similar Questions
Knowledge Check
For a particle moving in a straight line assume s,v,a and t represents displacement, velocity, acceleration and time respectively.
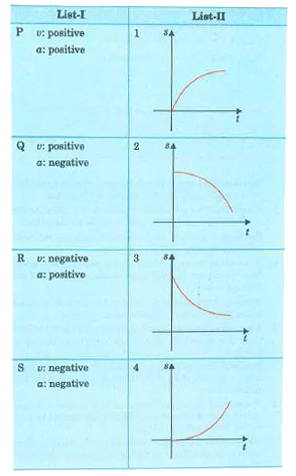 APQRS3241BPQRS1324CPQRS2134DPQRS4132
APQRS3241BPQRS1324CPQRS2134DPQRS4132If the displacement velocity and acceleration of a particle at time t be x,v and f respectively, then which one is true?
Af=v3d2tdx2Bf=−v3d2tdx2Cf=v2d2tdx2Df=−v2d2tdx2A particle moves according to the law x=t3−6t2+9t+5. The displacement of the particle at the time when its acceleration is zero, is
A9B-7C7D0
A particle moves in the x-y plane according to the law x=at, y=at (1−αt) where a and α are positive constants and t is time. Find the velocity and acceleration vector. The moment t0 at which the velocity vector forms angle of 90∘ with acceleration vector.
View SolutionA particle moves in the x-y plane according to the law x=at, y=at (1−αt) where a and α are positive constants and t is time. Find the velocity and acceleration vector. The moment t0 at which the velocity vector forms angle of 90∘ with acceleration vector.
View SolutionA particle moves along an arc of a circle of radius R according to the law l=asinωt, where l is the displacement from the initial position measured along the arc, and a and ω are constants. Assuming R=1.00m, a=0.80m, and ω=2.00rad/s, find:
(a) the magnitude of the total acceleration of the particle at the points l=0 and l=±a,
(b) the minimum value of the total acceleration wmin and the corresponding displacement lm.
View SolutionA particle moves in Xy plane according to the law X=asinωtandy=a(1−cosωt) where a and ω are constants. The particle traces-
View SolutionA particle is moving in a straight line according to graph given below : (a is acceleration, v is velocity, x is position, t is time) :
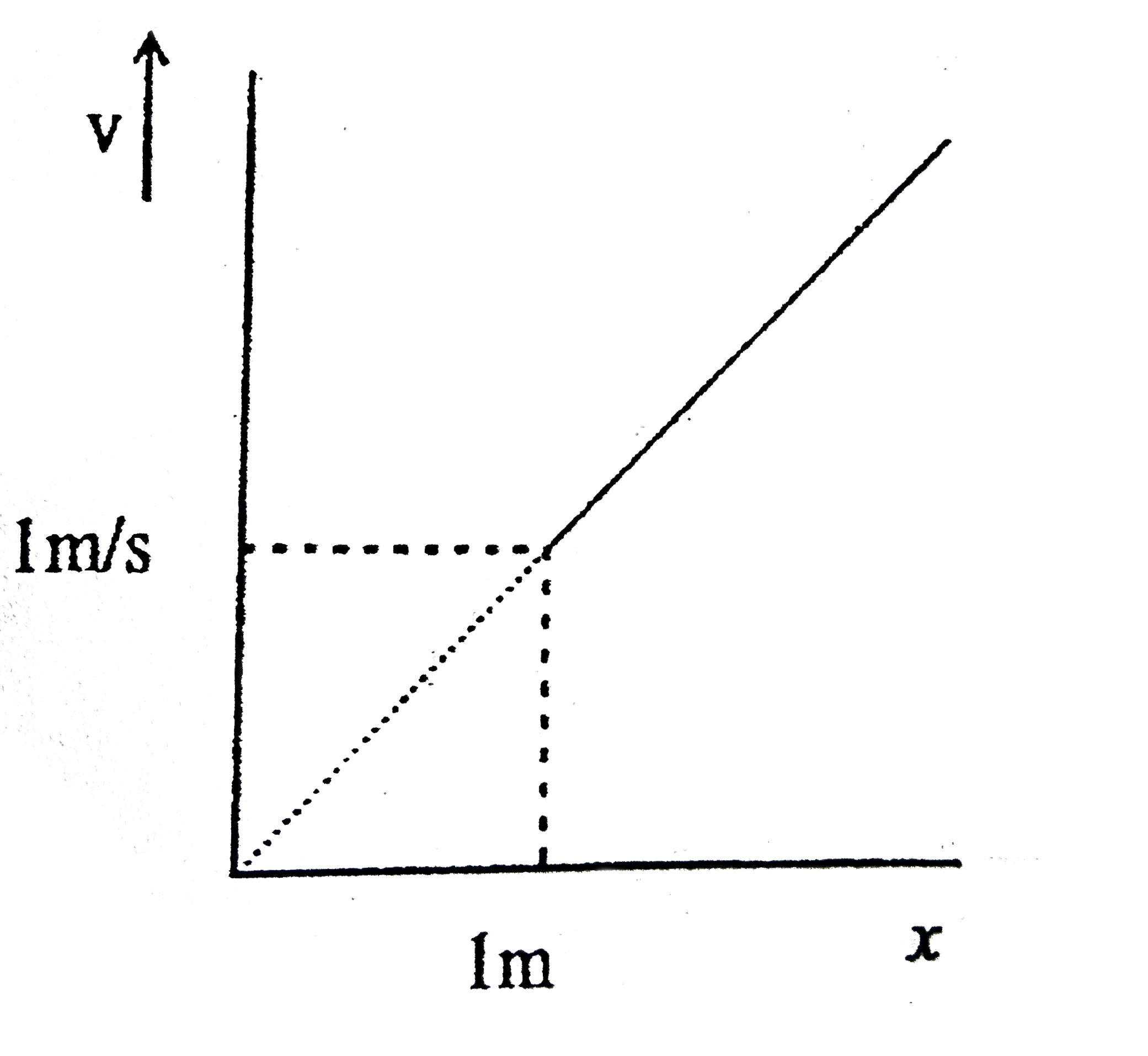
View Solution


