A system undergoes a cyclic process in which it absorbs heat Q1 and gives away heat Q2. If the efficiency of the process is η and the work done is W, then
W=Q1−Q2
η=WQ1
η=Q2Q1
η=1−Q2Q1
The correct Answer is:A, B, D
To solve the problem, we need to analyze the cyclic process of the system in terms of heat absorbed, heat given away, work done, and efficiency.
1. Understanding the Efficiency of the Process:
The efficiency (η) of a heat engine is defined as the ratio of the work done (W) by the engine to the heat absorbed (Q1) from the hot reservoir. Mathematically, this can be expressed as:
η=WQ1
2. Applying the First Law of Thermodynamics:
The first law of thermodynamics states that the change in internal energy (ΔU) of a system is equal to the heat added to the system (Q) minus the work done by the system (W):
ΔU=Q−W
For a cyclic process, the internal energy change over one complete cycle is zero (ΔU = 0). Therefore, we can rewrite the equation as:
0=Q−W⟹Q=W
3. Calculating the Net Heat Transfer:
In a cyclic process, the net heat transfer (Q_net) is the difference between the heat absorbed (Q1) and the heat rejected (Q2). Thus, we can express this as:
Qnet=Q1−Q2
Since we established that for a cyclic process, Q_net is equal to the work done (W), we can write:
W=Q1−Q2
4. Identifying the Correct Options:
From the above analysis, we can conclude:
- The efficiency is given by η=WQ1.
- The work done is equal to the net heat transfer, which is W=Q1−Q2.
Therefore, the correct options based on the analysis are:
- Option 1: Efficiency is η=WQ1 (Correct)
- Option 2: Work done is W=Q1−Q2 (Correct)
- Option 3: Qnet=W (Correct, as it follows from the first law of thermodynamics for cyclic processes)
Summary of Correct Options:
Thus, the correct answers are options 1, 2, and 4.
The efficiency (η) of a heat engine is defined as the ratio of the work done (W) by the engine to the heat absorbed (Q1) from the hot reservoir. Mathematically, this can be expressed as:
η=WQ1
The first law of thermodynamics states that the change in internal energy (ΔU) of a system is equal to the heat added to the system (Q) minus the work done by the system (W):
ΔU=Q−W
For a cyclic process, the internal energy change over one complete cycle is zero (ΔU = 0). Therefore, we can rewrite the equation as:
0=Q−W⟹Q=W
In a cyclic process, the net heat transfer (Q_net) is the difference between the heat absorbed (Q1) and the heat rejected (Q2). Thus, we can express this as:
Qnet=Q1−Q2
Since we established that for a cyclic process, Q_net is equal to the work done (W), we can write:
W=Q1−Q2
From the above analysis, we can conclude:
- The efficiency is given by η=WQ1.
- The work done is equal to the net heat transfer, which is W=Q1−Q2.
- Option 1: Efficiency is η=WQ1 (Correct)
- Option 2: Work done is W=Q1−Q2 (Correct)
- Option 3: Qnet=W (Correct, as it follows from the first law of thermodynamics for cyclic processes)
Thus, the correct answers are options 1, 2, and 4.
Topper's Solved these Questions
- PHYSICS PART2Book:FIITJEEChapter:PHYSICS PART2Exercise:Assertion-Reasoning MCQ
Explore 12 Videos
- PHYSICS PART2Book:FIITJEEChapter:PHYSICS PART2Exercise:Paragraph Based (MCQ)
Explore 3 Videos
- PHYSICS PART2Book:FIITJEEChapter:PHYSICS PART2Exercise:Section (II) : MCQ
Explore 27 Videos
- PHYSICS PART-IIIBook:FIITJEEChapter:PHYSICS PART-IIIExercise:NUMERICAL BASED QUESTIONS DECIMAL TYPE
Explore 11 Videos
- ROTATIONAL MECHANICSBook:FIITJEEChapter:ROTATIONAL MECHANICSExercise:COMPREHENSION - IV
Explore 2 Videos
Similar Questions
A system works in a cyclic process. It absorbs 20 calories of heat and rejects 60J of heat during the process. The magnitude of work done (J) is [1calorie=4.2J]:
View Solution
An ideal gas undergoes a cyclic process, in which one process is isochoric, one process is isothermal and one process is adiabatic. During the isothermal process, 40 J heat is released by the gas, and during the isochoric process, 80 J heat is absorbed by the gas. if work done by the gas during adiabatic process is W1 and during isothermal process is W2 then the magnitude of W1W2 will be equal to:
View Solution
Knowledge Check
A system undergoes a cyclic process in which it absorbs Q, heat and gives out Q2. heat. The efficiency of the process is n and the work done is W.
AW=Q1−Q2Bη=WQ1Cη=Q2Q1Dη=1−Q2Q1A system undergoes a cyclic process in which it absorbs Q1 heat and gives out Q2 heat. The efficiency of the process is η and work done is W. Select correct statement:
AW=Q1−Q2Bη=WQ1Cη=Q2Q1Dη=1−Q2Q1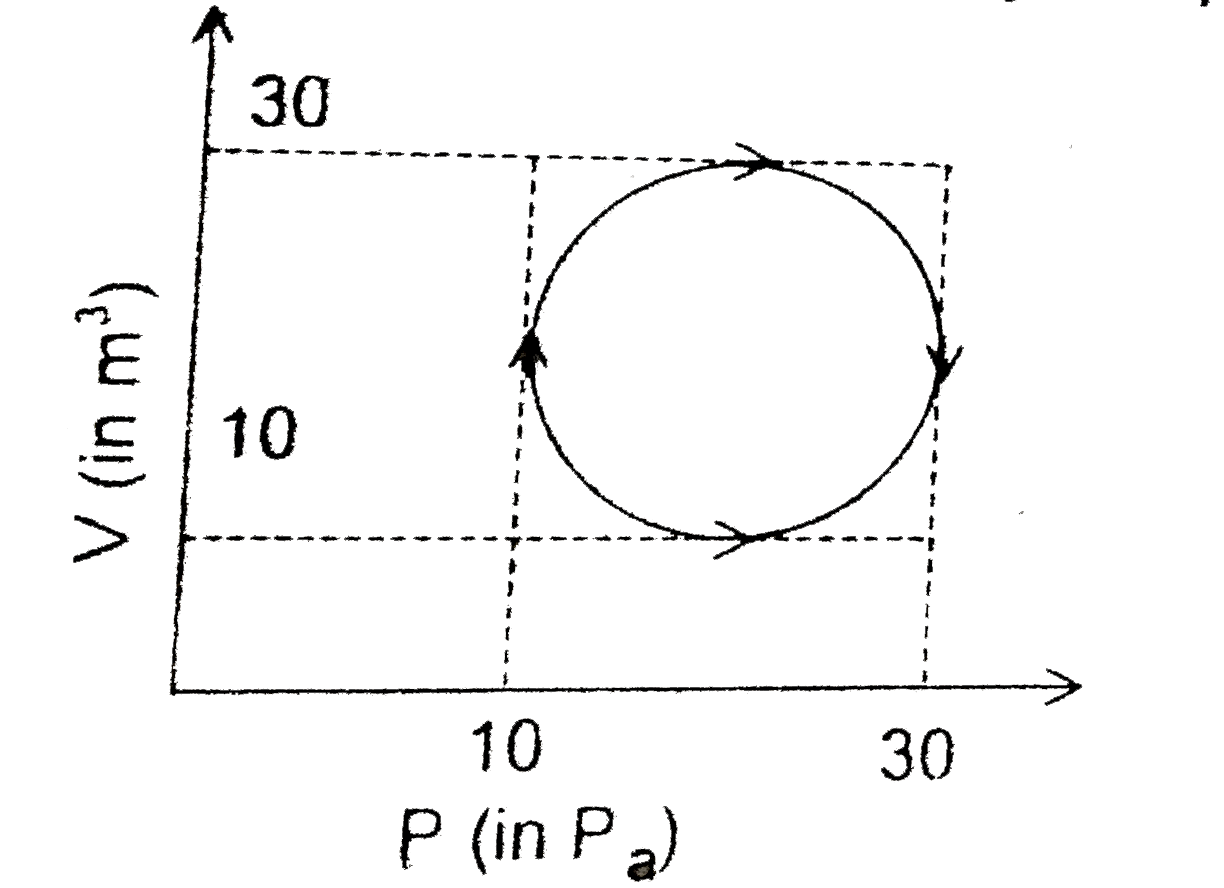
A system works under cyclic process as follow
Heat absorbed during the process isA227×102JB227×103JC227×104JD227×105J
In a cyclic process, work done by the system is
View SolutionIn a cyclic process, work done by the system is
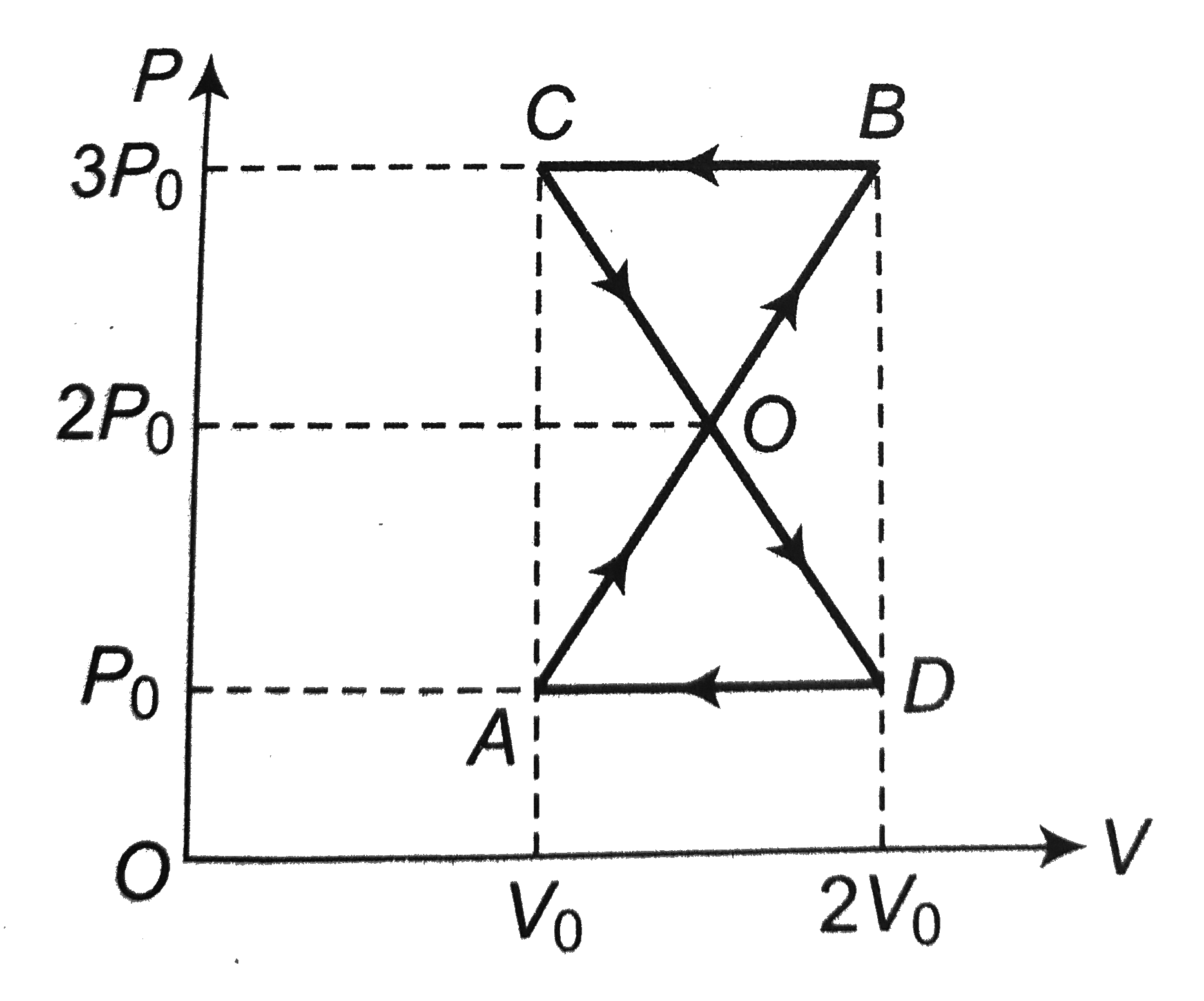
View SolutionA thermodynamic system undergoes cyclic process ABCDA as shown in figure. The work done by the system is
View SolutionA system absorbs 920 J of heat and does work. The change in internal energy (ΔU) for the process is 460 J. The work done by the system is
View SolutionA system absorbs 640 J heat and does work. The change in internal energy (ΔU) for the process is 380 J. The work done by the system is __ J
View Solution

