एक बेलन 30∘ कोण बनाते आनत तल पर लुढ़कता हुआ ऊपर चढ़ता है। आनत तल की तली में बेलन के द्रव्यमान केन्द्र की चाल 5m/s है।
(a) आनत तल पर बेलन कितना ऊपर जायेगा?
(b) वापस तली तक लौट आने में इसे कितना समय लगेगा?
(a) दिया गया है : θ=30∘,v=5मी से
माना कि बेलन नत तल पर h ऊँचाई तक जाता है। ऊर्जा संरक्षण के नियम से
12mv2+12Iω2=mgh
⇒12mv2+12(12mR2)v2R2=mgh
⇒12mv2+14mv2=mgh
⇒34mv2=mgh
⇒h=3v24g=3(5)24×9.8=1.913 मी.
यदि बेलन द्वारा नत तल के ऊपर की ओर तय दूरी s हो तो
s=hsinθजहाँ θ = आनत कोण
=1.913sin30∘=1.91312=3.83 मी.
(b) यदि बेलन द्वारा वापस तली तक लौट आने में लगा समय T हो तब
T=2t=2√2s(1+k2/R2)gsin0
=2√2×3.83(1+1/2)9.8sin30∘
=2√2×3.8×39.8=3.06 सेकंड
≈3.0 सेकंड
Topper's Solved these Questions
- कणों के निकाय तथा घूर्णी गति BOOK - SCIENCE PUBLICATIONCHAPTER - कणों के निकाय तथा घूर्णी गति EXERCISE - NCERT TEXT BOOK PROBLEMS (अतिरिक्त अभ्यास )
15 Videos
- कणों के निकाय तथा घूर्णी गति BOOK - SCIENCE PUBLICATIONCHAPTER - कणों के निकाय तथा घूर्णी गति EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (लघुत्तरात्मक प्रश्न )
11 Videos
- कणों के निकाय तथा घूर्णी गति BOOK - SCIENCE PUBLICATIONCHAPTER - कणों के निकाय तथा घूर्णी गति EXERCISE - बोधात्मक प्रश्न
16 Videos
- उष्मागतिकीBOOK - SCIENCE PUBLICATIONCHAPTER - उष्मागतिकीEXERCISE - अन्य महत्त्वपूर्ण प्रश्न (आंकिक प्रश्न)
28 Videos
- कार्य, ऊर्जा एवं शक्ति BOOK - SCIENCE PUBLICATIONCHAPTER - कार्य, ऊर्जा एवं शक्ति EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (आंकित प्रश्न ) टक्करों पर आधारित प्रश्न
8 Videos
Similar Questions
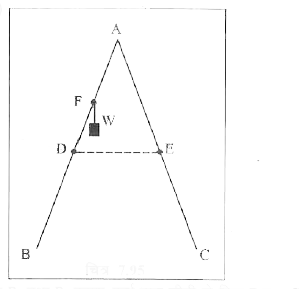
जैसा चित्र में दिखाया गया है, एक खड़ी होने वाली सीढ़ी के दो पक्षों BA और CA की लम्बाई 1.6m है और इनको A पर कब्जा लगाकर जोड़ा गया है। इन्हें ठीक बीच में 0.5m लम्बी रस्सी DE द्वारा बांधा गया है। सीढ़ी BA के अनुदिश B से 1.2m की दूरी पर स्थित बिन्दु F से 40kg का एक भार लटकाया गया है। यह मानते हुए कि फर्श घर्षण रहित है और सीढ़ी का भार उपेक्षणीय है, रस्सी में तनाव और सीढी पर फर्श द्वारा लगाया गया बल ज्ञात कीजिए। (g=9.8 m/S2 लीजिए)
View Solutionद्रव्यमान केन्द्र क्या है? क्या किसी वस्तु के द्रव्यमान केन्द्र पर द्रव्यमान का होना आवश्यक है ?
View Solutionकिसी भी पिण्ड का जड़त्व आघूर्ण का मान किसी अक्ष के परितः कब न्यूनतम होता है?
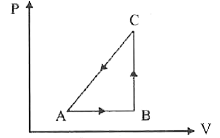
View Solutionएक निकाय का P-V आरेख जो कि ऊष्मागतिकी परिवर्तन प्रदर्शित करता है। चित्र में दर्शाया गया है। निकाय पर किया गया कार्य A→B→C 50J है ,आंतरिक ऊर्जा में परिवर्तन ज्ञात कीजिये,दी गई ऊष्मा 84 J है।
View Solutionदो किलोग्राम द्रव्यमान का एक पिण्ड किसी अन्य स्थिर पिण्ड से पूर्णतः अप्रत्यास्थ टक्कर करता है। यदि टक्कर के बाद दोनों पिण्ड उसी दिशा में पहले पिण्ड की एक चौथाई चाल से गतिमान हो तो दुसरे पिण्ड का द्रव्यमान ज्ञात करिये।
View Solutionएकसमान विद्युत क्षेत्र E=3×103ˆi(N)/C पर विचार कीजिये ।
(a) इस क्षेत्र का 10 cm भुजा के वर्ग के उस पार्श्व से जिसका तल yz तल के समांतर है, गुजरने वाला फ्लक्स क्या है ?
(b) इस वर्ग से गुजरने वाला फ्लक्स कितना है यदि इसके तल का अभिलंब x- अक्ष से 60∘ कोण बनता है ?
View Solutionआनत तल पर वस्तु की गति
View Solutionआनत घर्षण वाले तल पर वस्तु की गति -1
View Solutionआनत घर्षण वाले तल पर वस्तु की गति -2
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionघर्षण कोण | समतल सतह पर वस्तु की गति | आनत तल पर वस्तु की गति
View Solutionघर्षण रहित नत तल पर रखे गुटके की गति
View Solutionघर्षण रहित नत तल पर रखे गुटकों की गति
View Solutionभूमिका |निर्देशांक तल #!#अंतरिक्ष में एक बिंदु के निर्देशांक#!#अष्टांश
View Solutionनत तल पर घर्षण
View Solutionयदि कोई बिंदु P,yz तल में स्थित है तो yz तल में उस बिंदु के निर्देशांक ___________के रूप में होंगे
View Solution
