सिद्ध करो कि -
(→A×→B)2+(→A.→B)2=A2B2
(→A×→B)2+(→A.→B)2
=(ABsinθ.ˆn)2+(ABcosθ)2
=A2B2sin2θ+A2B2cos2θ
(∴ˆn.ˆn=1)
=A2B2(sin2θ+cos2θ)
=A2B2
Topper's Solved these Questions
- कणों के निकाय तथा घूर्णी गति BOOK - SCIENCE PUBLICATIONCHAPTER - कणों के निकाय तथा घूर्णी गति EXERCISE - TEST YOUR KNOWLEDGE
20 Videos
- कणों के निकाय तथा घूर्णी गति BOOK - SCIENCE PUBLICATIONCHAPTER - कणों के निकाय तथा घूर्णी गति EXERCISE - MCQs
11 Videos
- उष्मागतिकीBOOK - SCIENCE PUBLICATIONCHAPTER - उष्मागतिकीEXERCISE - अन्य महत्त्वपूर्ण प्रश्न (आंकिक प्रश्न)
28 Videos
- कार्य, ऊर्जा एवं शक्ति BOOK - SCIENCE PUBLICATIONCHAPTER - कार्य, ऊर्जा एवं शक्ति EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (आंकित प्रश्न ) टक्करों पर आधारित प्रश्न
8 Videos
Similar Questions
घूर्णन गति से क्या तात्पर्य है?
View Solutionयदि HCI अणु में H' की द्रव्यमान-केन्द्र से दूरी x हो तो CI35 की दूरी होगी
View Solutionएक निकाय का P-V आरेख जो कि ऊष्मागतिकी परिवर्तन प्रदर्शित करता है। चित्र में दर्शाया गया है। निकाय पर किया गया कार्य A→B→C 50J है ,आंतरिक ऊर्जा में परिवर्तन ज्ञात कीजिये,दी गई ऊष्मा 84 J है।
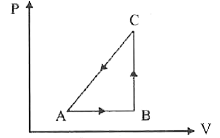
View Solutionदो किलोग्राम द्रव्यमान का एक पिण्ड किसी अन्य स्थिर पिण्ड से पूर्णतः अप्रत्यास्थ टक्कर करता है। यदि टक्कर के बाद दोनों पिण्ड उसी दिशा में पहले पिण्ड की एक चौथाई चाल से गतिमान हो तो दुसरे पिण्ड का द्रव्यमान ज्ञात करिये।
View SolutionIf →aand→b are two vectors, such that ∣∣→a×→b∣∣=2 , then find the value of [→a→b→a×→b]
View SolutionProve that ∣∣→a×→b∣∣2=∣∣∣→a⋅→a→a⋅→b→a⋅→b→b⋅→b∣∣∣.
View Solutionसदिशों तथा के लिए सिद्ध कीजिए कि
∣∣→a×→b∣∣2=∣∣∣→a.→a→a.→b→a.→b→a.→b∣∣∣
View Solutionसिद्ध कीजिए कि (→a×→b)=a2b2−(→a⋅→b)2.
View Solutionसिद्ध कीजिए :
(i) (→A+→B)−(→A−→B)2=4(→A⋅→B).
(ii) (→A+→B)×(→A−→B)=−2(→A×→B).
(iii) (→A×→B)2+(→A⋅→B)2=A2B2.
View Solutionसिद्ध कीजिए कि ∣∣→A×→B∣∣2+∣∣→A⋅→B∣∣2=(AB)2.
View Solutionदर्शाइए कि (→a−→b)×(→a+→b)=2(→a×→b)
View SolutionShow that (→a×→b)2=|→a|2∣∣→b∣∣2−(→a.→b)2=∣∣∣→a.→a→a.→b→a.→b→b.→b∣∣∣
View Solutionপ্রমাণ করাে যে, (→a–→b)×(→a+→b)=2(→a×→b)
View SolutionIf →aand→b are two vectors, such that ∣∣→a×→b∣∣=2 , then find the value of [→a→b→a]×→b .
View Solutionसिद्ध कीजिए कि ∣∣→A×→B∣∣2+∣∣→A⋅→B∣∣2=(AB)2.
View Solution(→a−→b)×(→a+→b) is equal to a)→a b)|→a|2−∣∣→b∣∣2 c)→a×→b d)2(→a×→b)
View Solution
