How many times does the graph of y=x3−3x2−x+3 intersects the x - axis :
1
2
3
none of these
The correct Answer is:C
To determine how many times the graph of the function y=x3−3x2−x+3 intersects the x-axis, we need to find the roots of the equation y=0. This means we need to solve the polynomial equation:
x3−3x2−x+3=0
Step 1: Find a root of the polynomial
We can start by testing some simple values of x to see if they yield y=0.
Let's try x=1:
y=13−3(12)−1+3=1−3−1+3=0
Since y=0 when x=1, we have found one root: x=1.
Step 2: Factor the polynomial
Since x=1 is a root, we can factor the polynomial using (x−1). We will perform polynomial long division to divide x3−3x2−x+3 by (x−1).
1. Divide x3 by x to get x2.
2. Multiply (x−1) by x2 to get x3−x2.
3. Subtract (x3−x2) from (x3−3x2) to get −2x2.
4. Bring down the next term, resulting in −2x2−x+3.
5. Divide −2x2 by x to get −2x.
6. Multiply (x−1) by −2x to get −2x2+2x.
7. Subtract (−2x2+2x) from (−2x2−x) to get −3x+3.
8. Bring down the next term, resulting in −3x+3.
9. Divide −3x by x to get −3.
10. Multiply (x−1) by −3 to get −3x+3.
11. Subtract to get 0.
Thus, we have:
x3−3x2−x+3=(x−1)(x2−2x−3)
Step 3: Factor the quadratic
Next, we need to factor the quadratic x2−2x−3. We can factor it as follows:
x2−2x−3=(x−3)(x+1)
Step 4: Write the complete factorization
Now we can write the complete factorization of the polynomial:
y=(x−1)(x−3)(x+1)
Step 5: Find the roots
To find the x-intercepts (roots), we set each factor equal to zero:
1. x−1=0 gives x=1
2. x−3=0 gives x=3
3. x+1=0 gives x=−1
Conclusion
The roots of the polynomial are x=1,x=3, and x=−1. Therefore, the graph of the function intersects the x-axis three times.
Final Answer
The graph of y=x3−3x2−x+3 intersects the x-axis 3 times.
---
We can start by testing some simple values of x to see if they yield y=0.
Since x=1 is a root, we can factor the polynomial using (x−1). We will perform polynomial long division to divide x3−3x2−x+3 by (x−1).
2. Multiply (x−1) by x2 to get x3−x2.
3. Subtract (x3−x2) from (x3−3x2) to get −2x2.
4. Bring down the next term, resulting in −2x2−x+3.
5. Divide −2x2 by x to get −2x.
6. Multiply (x−1) by −2x to get −2x2+2x.
7. Subtract (−2x2+2x) from (−2x2−x) to get −3x+3.
8. Bring down the next term, resulting in −3x+3.
9. Divide −3x by x to get −3.
10. Multiply (x−1) by −3 to get −3x+3.
11. Subtract to get 0.
Next, we need to factor the quadratic x2−2x−3. We can factor it as follows:
Now we can write the complete factorization of the polynomial:
To find the x-intercepts (roots), we set each factor equal to zero:
2. x−3=0 gives x=3
3. x+1=0 gives x=−1
The roots of the polynomial are x=1,x=3, and x=−1. Therefore, the graph of the function intersects the x-axis three times.
The graph of y=x3−3x2−x+3 intersects the x-axis 3 times.
Topper's Solved these Questions
- FUNCTIONS AND GRAPHBOOK - ARIHANT SSCCHAPTER - FUNCTIONS AND GRAPHEXERCISE - Final Round
40 Videos
- FUNCTIONS AND GRAPHBOOK - ARIHANT SSCCHAPTER - FUNCTIONS AND GRAPHEXERCISE - EXERCISE(LEVEL 1)
84 Videos
- ELEMENTS OF ALGEBRABOOK - ARIHANT SSCCHAPTER - ELEMENTS OF ALGEBRAEXERCISE - EXERCISE(LEVEL 1)
32 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 2
40 Videos
Similar Questions
Knowledge Check
Sketch the graph of y=x33−3x22+2x+6
A B
B C
C DNone of these
DNone of theseFind the value of y where the graph of 3x2+19×−18=0 intersects the Y-axis.
A−18B0C4D16
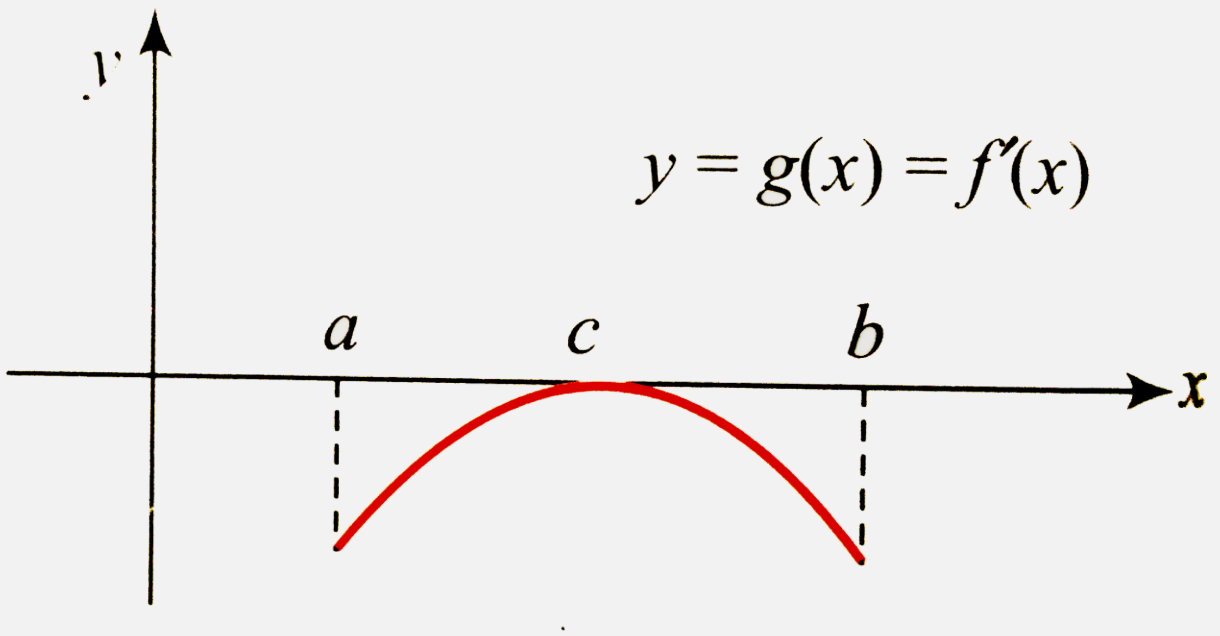
Following is the graph of y = f' (x) , given that f(c) = 0. Analyse the graph and answer the following questions.
(a) How many times the graph of y = f(x) will intersect the x - axis?
(b) Discuss the type of roots of the equation f (x) = 0, a≤x≤b.
(c) How many points of inflection the graph of y=f(x),a≤x≤b, has?
(d) Find the points of local maxima/minima ofy=f(x),a<xb.
(e) How many roots equation f''(x)=0 has?
View SolutionGraph of y=−x3+6x2−11x+6
View SolutionIn how many points the graph of f(x)=x3+2x2+3x+4 meets the x-axis ?
View SolutionDraw the graph of y=(x2−x5)(x−2)3.
View SolutionDraw graph of y=x3−5xx2+1.
View SolutionDraw the graph of |y|=(x−1)(x−2)(x−3).
View Solution
