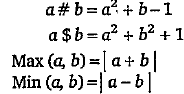a#b=a2+b−1
a$b=a2+b2+1
Max (a,b)=|a+b|
Min (a, b)=|a−b|
Max [Min (1$2),(2$3)),Max ((3#4),(4#5))] is equal to :
A
24
B
40
C
42
D
none of these
Video Solution
Text Solution
The correct Answer is:B
|
Answer
Step by step video, text & image solution for a#b=a^(2)+b-1 a$b=a^(2)+b^(2)+1 "Max (a,b)"=|a+b| "Min (a, b)"=|a-b| Max ["Min "(1$2),(2$3)),"Max "("(3#4),(4#5)")] is equal to : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FUNCTIONS AND GRAPHBook:ARIHANT SSCChapter:FUNCTIONS AND GRAPHExercise:EXERCISE(LEVEL 2)
Explore 48 Videos
- FUNCTIONS AND GRAPHBook:ARIHANT SSCChapter:FUNCTIONS AND GRAPHExercise:Final Round
Explore 40 Videos
- FUNCTIONS AND GRAPHBook:ARIHANT SSCChapter:FUNCTIONS AND GRAPHExercise:INTRODUCTORY EXERCISE - 17.3
Explore 17 Videos
- ELEMENTS OF ALGEBRABook:ARIHANT SSCChapter:ELEMENTS OF ALGEBRAExercise:EXERCISE(LEVEL 1)
Explore 32 Videos
- FUNDAMENTALS Book:ARIHANT SSCChapter:FUNDAMENTALS Exercise:TEST OF YOU - LEARNING - 2
Explore 40 Videos
Similar Questions
Knowledge Check
a#b=a2+b−1
a$b=a2+b2+1
Max (a,b)=|a+b|
Min (a, b)=|a−b|
Find the value of Min [(1#2)$3,4#(5$6)]$ Max (6#7),(7#8)]:A13574B14573C13575D14674a#b=a2+b−1
a$b=a2+b2+1
Max (a,b)=|a+b|
Min (a, b)=|a−b|
Max [(2#3)$(3#4),(4$4)] is equal to :Aa. 1234Bb. 1236Cc. 1335Dd. none of theseFor any natural number p and q (i) p # q = p 3 + q 3 + 3 and p ∗ q = p 2 + q 2 + 2 and p $ q = | p − q | (ii) Max (p,q) = Maximum of (p,q) and Min (p and q) = Minimum of (p,q) .The value of [Max(2,4)$Min(6,8)]#[Min(10,12)$Max(14,16)]
Aa.227Bb. 225Cc. 224Dd. None of these
If f(a,b)=a+b2
g(a,b)=a2+b2
h(a,b)=max (a,b)
Find the value of f(g(3,9)),h(−1,1)
View SolutionIf 5−(3a−2b)2 will be maxm, when ab= ?
View SolutionThe value of [Max(2,4)$Min(6,8)]#[Min(10,12)$Max(14,16)]
View SolutionIf a+b=1 then a4+b4−a3−b3−2a2b2+ab is equal to
View SolutionIf A:B=12:13, B:C=15:13, then (A+B):(B+C) is equal to :
View Solution