If the graph of the function f(x)=ax−1xn(ax+1) is symmetric about y - axis, then n is equal to :
a.−13
b. 14
c. 2/3
d. 2
The correct Answer is:A
To determine the value of n such that the function
f(x)=ax−1xn(ax+1)
is symmetric about the y-axis, we need to check if the function is even. A function is even if f(x)=f(−x).
1. Find f(−x):
We start by substituting −x into the function:
f(−x)=a−x−1(−x)n(a−x+1)
Simplifying this, we have:
f(−x)=1ax−1(−x)n(1ax+1)
This can be rewritten as:
f(−x)=1−ax(−x)n(1+ax)
2. Simplify f(−x):
To simplify further, multiply the numerator and denominator by ax:
f(−x)=ax(1−ax)(−x)n(1+ax)ax=ax−a2x(−x)n(ax+1)
3. Set f(x) equal to f(−x):
For the function to be even, we need:
ax−1xn(ax+1)=ax−a2x(−x)n(ax+1)
Since ax+1 is common in both denominators, we can cancel it (assuming ax+1≠0):
ax−1=(ax−a2x)(−x)n⋅xn
4. Cross-multiply:
Rearranging gives:
(ax−1)(−x)n=ax−a2x
5. Analyze the equation:
For the equation to hold for all x, the powers of x must match. The left side has a term of (−x)n which indicates that n must be odd for the left side to be equal to the right side when x is negative.
6. Conclusion:
Since (−1)n=−1 when n is odd, we conclude that n must be an odd integer for the function to be symmetric about the y-axis.
Result:
Thus, the value of n is equal to 1.
We start by substituting −x into the function:
f(−x)=a−x−1(−x)n(a−x+1)
Simplifying this, we have:
f(−x)=1ax−1(−x)n(1ax+1)
This can be rewritten as:
f(−x)=1−ax(−x)n(1+ax)
To simplify further, multiply the numerator and denominator by ax:
f(−x)=ax(1−ax)(−x)n(1+ax)ax=ax−a2x(−x)n(ax+1)
For the function to be even, we need:
ax−1xn(ax+1)=ax−a2x(−x)n(ax+1)
Since ax+1 is common in both denominators, we can cancel it (assuming ax+1≠0):
ax−1=(ax−a2x)(−x)n⋅xn
Rearranging gives:
(ax−1)(−x)n=ax−a2x
For the equation to hold for all x, the powers of x must match. The left side has a term of (−x)n which indicates that n must be odd for the left side to be equal to the right side when x is negative.
Since (−1)n=−1 when n is odd, we conclude that n must be an odd integer for the function to be symmetric about the y-axis.
Thus, the value of n is equal to 1.
Topper's Solved these Questions
- FUNCTIONS AND GRAPHBook:ARIHANT SSCChapter:FUNCTIONS AND GRAPHExercise:INTRODUCTORY EXERCISE - 17.3
Explore 17 Videos
- FUNCTIONS AND GRAPHBook:ARIHANT SSCChapter:FUNCTIONS AND GRAPHExercise:EXERCISE(LEVEL 1)
Explore 84 Videos
- FUNCTIONS AND GRAPHBook:ARIHANT SSCChapter:FUNCTIONS AND GRAPHExercise:INTRODUCTORY EXERCISE - 17.1
Explore 44 Videos
- ELEMENTS OF ALGEBRABook:ARIHANT SSCChapter:ELEMENTS OF ALGEBRAExercise:EXERCISE(LEVEL 1)
Explore 32 Videos
- FUNDAMENTALS Book:ARIHANT SSCChapter:FUNDAMENTALS Exercise:TEST OF YOU - LEARNING - 2
Explore 40 Videos
Similar Questions
Knowledge Check
The graph of the function y=loga(x+√x2+1) is not symmetric about the origin.
ATrueBFalseCCan't sayDInsufficient dataIf the real valued function f(x)=ax−1xn(ax+1) is even, then n is equal to
A2B44257C44287D3If the real valued function f(x)=ax−1xn(ax+1) is even, then n is equal to
A2B44257C44287D3
If the graph of the function
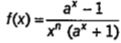 is symmetric about y-axis, then n is equal to :
is symmetric about y-axis, then n is equal to :
View SolutionA function whose graph is symmetric about y-axis is
View SolutionIf the graph of the function y = f(x) is symmetrical about the line x = 2, then
View SolutionThe graph of the function y=f(x) is symmetrical about the line x=2, then :
View SolutionThe graph of the function y=f(x) is symmetrical about the line x=2, then :
View Solution
