आपको क्राउन काँच का बना एक उभयोत्तल लेन्स दिया गया है जिसके प्रत्येक पृष्ठ का वक्रता व्यासार्ध, 15 cm है | इस लेन्स के एक पृष्ट पर एक फ्लिंट काँच के लेन्स का रोपण किया जाता है | फ्लिंट काँच के लेन्स के दूसरे पृष्ठ का वक्रता व्यासार्ध क्या हो कि संयोजन, नीले और लाल प्रकाश के लिए अवर्णिक (जोड़ा) बने? अपवर्तनांकों के आवश्यक आँकड़े अध्याय 13 की विषय-आधारित समस्या 16 के उत्तर से प्राप्त करें |
क्राउन काँच के लेन्स के लिए
1f=(μ−1)(1R1−1R2)=(μ−1)(115−1−15)
या 1f=(μ−1)(215)
(क्योंकि लेन्स उत्तल है, इसलिए R1=+15 cm और R2=−15 cm)
इस प्रकार 1fb−1fr=(μb−1)(215)−(μr−1)(215)
=(μb−μr)(215)
=(1.5200−1.5090)(215)=0.0014 ...(i)
इसी प्रकार फ्लिंट काँच के लेन्स के लिए
1f.b−1f.r=(μ.b−1)(1R.1−1R.2)−(μ.r−1)(1R.1−1R.2)
या (1f.b−1f.r)=(μ.b−μ.r)(1R.2−1R.1)
क्योंकि फ्लिंट काँच के लेन्स का वह पृष्ठ, जिसका क्राउन काँच के लेन्स पर रोपण किया गया है, अवतल है, इसलिए R.1=−15 cm है |
इस प्रकार (1f.b−1f.r)=(1.6658−1.6443)(1−15−1R.2)
=−(0.0215)(115+1R.2)
या (1f.b−1f.r)=−0.0014−0.0215R.2 ...(ii)
अवर्णक जोड़े के लिए
(1fb−1fr)+(1f.b−1f.r)=0
समीकरण (i) और (ii) से हम पते हैं
0.0014−0.0014−0.0215R.2=0
या 0.0215R.2=0 या R.2=∞
अर्थात पृष्ठ समतल है | इस प्रकार फ्लिंट काँच का लेन्स, समतल-अवतल है |
Topper's Solved these Questions
- गोलीय पृष्ठों और लेन्सों पर अपवर्तन Book:GRB PUBLICATION HINDIChapter:गोलीय पृष्ठों और लेन्सों पर अपवर्तन Exercise:उच्चस्तरीय चिंतन: प्रश्नोत्तरी
Explore 10 Videos
- गोलीय पृष्ठों और लेन्सों पर अपवर्तन Book:GRB PUBLICATION HINDIChapter:गोलीय पृष्ठों और लेन्सों पर अपवर्तन Exercise:प्रश्नोत्तरी : 1 अंक
Explore 16 Videos
- गोलीय पृष्ठों और लेन्सों पर अपवर्तन Book:GRB PUBLICATION HINDIChapter:गोलीय पृष्ठों और लेन्सों पर अपवर्तन Exercise:विषय-आधारित समस्याएँ: हल सहित (लेन्स और दर्पण का संयोजन)
Explore 2 Videos
- इलेक्ट्रॉनिक युक्तियाँ Book:GRB PUBLICATION HINDIChapter: इलेक्ट्रॉनिक युक्तियाँ Exercise:विषय -आधारित अभ्यास
Explore 31 Videos
- चुम्बकत्वBook:GRB PUBLICATION HINDIChapter:चुम्बकत्वExercise:प्रतियोगिता सामग्री रिक्त स्थान भरना
Explore 12 Videos
Similar Questions
दो बिल्कुल समरूप काँच की फ़्लास्कों में से एक जल से भरी जाती है और दूसरी स्पिरिट से। दोनों फ़्लास्कों पर कस कर ढक्कन लगा दिया जाता है। एक टेबल लैम्प की सहायता से बिना फ्लास्कों के ढक्कन खोले आप कैसे निश्चित करेंगे कि कौन सी जल से भरी है और किस में स्पिरिट है?
View Solutionक्या ज़रूरी है कि जिस लेन्स की एक माध्यम से घिरे होने पर फ़ोकस दूरी धनात्मक हो, उस की फ़ोकस दूरी किसी दूसरे माध्यम से घिरे होने पर भी धनात्मक ही होगी?
View Solutionचित्र 14.36 में दिखाए अनुसार मोमबत्ती, 10 cm फ़ोकस दूरी वाले अवतल दर्पण के वक्रता केन्द्र पर है | अभिसारी लेन्स की फ़ोकस दूरी 32 cm है और यह मोमबत्ती के दाईं ओर 85 cm की दूरी पर है | मोमबत्ती, दाईं ओर से लेन्स में से देखी जाती है | लेन्स, मोमबत्ती के दो प्रतिबिम्ब बनाता है दूसरा प्रतिबिम्ब, उस प्रकाश से बनता है जो मोमबत्ती से दर्पण की ओर जाता है, परावर्तित होता है और फिर लेन्स में से गुज़रता है |
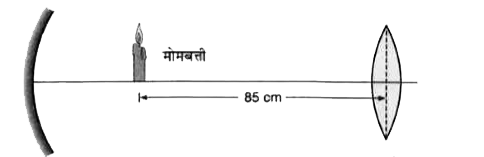
(a) इन दोनों प्रतिबिम्बों के लिए एक मुख्य किरण चित्र बनाएँ जो प्रतिबिम्ब की स्थिति बताए |
(b) हर प्रतिबिम्ब के लिए निम्न प्रश्नों के उत्तर दें :
(i) प्रतिबिम्ब कहाँ है ?
(ii) क्या प्रतिबिम्ब, वास्तविक है या आभासी ?
(iii) या प्रतिबिम्ब, मूल वस्तु के सापेक्ष सीधा है या उलटा ?
View Solutionएक मादित अर्धचालक में अशुद्धता स्तर, चालन बैंड के 30 MeV नीचे हैं।
(a) क्या पदार्थ , n-प्रकार का है या p-प्रकार का ?
(b) किसी ऊष्मीय टक्कर में ऊर्जा की मात्रा kBT(−30meV), अशुद्धता आयन से शिथिल रूप से बंधे अतिरिक्त इलेक्ट्रान को दी जाती है और यह इलेक्ट्रॉन, चालन बैंड में छलांग लगाने भर के योग्य हो जाता है। ताप T निकालें।
View Solutionएक छड़ चुम्बक को इसकी लम्बाई के लम्बवत दो बराबर टुकड़ों में काटने से एक ही ध्रुव तीव्रता परन्तु.........द्विध्रुव आघूर्ण वाले चुम्बक उत्पन्न होते हैं।
View Solutionकाँच के प्रिज्म द्वारा श्वेत प्रकाश का विक्षेपण
View Solutionएक वृत्त के अंतर्गत बने समबहुभुज की प्रत्येक भुजा केंद्र पर 45∘ का कोण बनाती है| बहुभुज का नाम दीजिए |
View Solutionस्पीति के इतिहास का एक बड़ा कारक क्या है
View Solution.0.12 मी फोकस, दूरी के उत्तल लेन्स से वस्तु का तीन गुना वास्तविक प्रतिबिम्ब पर्दे पर प्राप्त करने के लिए वस्तु को लेन्स से दूर रखना
View SolutionWhich type of glass is used for making glass reinforced plastic? च प्रबलित प्लास्टिक बनाने के लिए किस प्रकार के काँच का प्रयोग किया जाता है?
View Solutionदो गैसों का एक भूरे रंग का मिश्रण धातु कॉपर के साथ 6N नाइट्रिक अम्ल के अपचयन से प्राप्त किया जाता है। शीतलन पर यह मिश्रण एक नीले द्रव में संघनित होता है, जो -30^@C पर जमने पर एक नीला ठोस देता है। नीले द्रव या ठोस के लिए सही विकल्प है:
View Solutionएक आदर्श गैस के लिए चक्र के सिरों पर दिखाए गए परिवर्तन की एक श्रेणी के माध्यम से किया गया कुल कार्य निम्न के बराबर है:
View Solution27^@ C और 760 टॉर पर N_2O_4 के 20 % अणुओं को गैस के एक नमूने में वियोजित किया जाता है | साम्य पर मिश्रण का घनत्व क्या होगा ?
View Solutionनिम्नलिखित यौगिक के जल अपघटित उत्पादों में से एक, काँच पात्र की सिलिका के साथ अभिक्रिया नहीं करता है?
View Solutionफॉर्मेल्डिहाइड और एसीटैल्डिहाइड के मध्य विभेद करने के लिए किस अभिकर्मक का उपयोग किया जाता है?
View Solutionजल के एक पूल के तल में एक गोताखोर द्वारा मुक्त किया गया वायु का एक बुलबुला जल के पृष्ठ के करीब पहुंचते ही बड़ा हो जाता है। मान लीजिए कि तापमान स्थिर है और सही कथन का चयन कीजिए। बुलबुले के अंदर का दाब है-
View Solution

