12cm भुजा वाला एक वर्गाकार लूप, जिसकी भुजाएँ X और Y अक्षों के समान्तर हैं, 8 cm/s के वेग से धनात्मक X-दिशा में ऐसे स्थान में चलाया जाता है जिसमें धनात्मक Z-दिशा में चुम्बकीय क्षेत्र है। क्षेत्र न तो आकाश में एकसमान है और न ही समय के साथ स्थिर। इसकी प्रवणता ऋणात्मक X-दिशा में है (अर्थात् ज्यों ज्यों ऋणात्मक X-दिशा में जाएँ, यह बढ़ता है) और यह समय के साथ की दर से घट रहा है। लूप में प्रेरित धारा की दिशा और परिमाण निकालें यदि इसका प्रतिरोध हो।
यहाँ लूप का क्षेत्रफल
(ऋणात्मक X-दिशा में बढ़ता है)
(समय के साथ घटता है)
x के साथ B में परिवर्तन से प्रेरित विद्युत वाहक बल
लेन्ज के नियम के अनुसार , धनात्मक Z-दिशा में फ्लक्स में कमी उत्पन्न करता है क्योंकि लूप उस धनात्मक X-दिशा में चल रहा है जिसमें क्षेत्र घटता है।
t के साथ B में परिवर्तन से प्रेरित विद्युत वाहक बल
भी धनात्मक Z-दिशा में फ्लक्स में कमी उत्पन्न करता है जब यह समय के साथ घटता है।
क्योंकि और दोनों फ्लक्स में कमी उत्पन्न करते हैं, इसलिए कुछ प्रेरित विद्युत वाहक बल
प्रेरित धारा
क्योंकि , धनात्मक Z-दिशा में फ्लक्स में कमी उत्पन्न करता है, इसलिए प्रेरित विद्युत वाहक बल की दिशा ऐसी है कि यह धनात्मक Z-दिशा में लूप में से फ्लक्स बढ़ाती है अर्थात् यह वामावर्त दिशा में है यदि लूप दाईं ओर चलता है।
Topper's Solved these Questions
- वैद्युतचुम्बकीय प्रेरण BOOK - GRB PUBLICATION HINDICHAPTER - वैद्युतचुम्बकीय प्रेरण EXERCISE - NCERT पाठ्यपुस्तक अभ्यास: उत्तरों सहित
8 Videos
- वैद्युतचुम्बकीय तरंगे BOOK - GRB PUBLICATION HINDICHAPTER - वैद्युतचुम्बकीय तरंगे EXERCISE - प्रतियोगिता साम्रगी रिक्त स्थान भरना
10 Videos
- वैधुत आवेश BOOK - GRB PUBLICATION HINDICHAPTER - वैधुत आवेश EXERCISE - विषय-आधारित अभ्यास
24 Videos
Similar Questions
निम्न चित्रों 1(a) से (f) में दर्शाई गई स्थितियों में प्रेरित धारा की दिशा बताएँ।
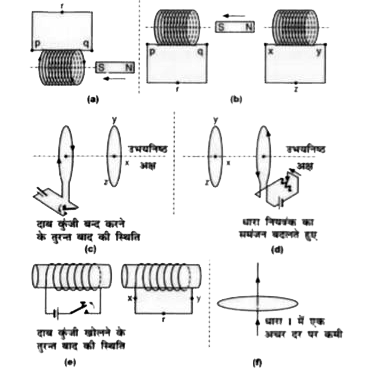
View Solutionकिसी वैद्युतचुम्बकीय तरंग में आयाम E0 और B0 ___ होते हैं परन्तु मैक्सवेल के समीकरण के अनुसार ___ द्वारा सम्बन्धित होते हैं।
View Solutionएक वस्तु पर −1.00×10−10C का नेट आवेश है। इसमें कितने अतिरिक्त इलेक्ट्रॉन है ?
View Solution12 सेमी भुजा वाला वर्गाकार लूप जिसकी भुजाएँ X एवं Y अक्षो के समांतर है x - दिशा में 8 सेमी से−1 की गति से चलाया जा रहा है । लूप तथा उसकी गति का परिवेश धनात्मक z दिशा के चुम्बकीय क्षेत्र का है । चुम्बकीय क्षेत्र न तो एकसमान है और न ही समय के साथ नियत है । इस क्षेत्र की ऋणात्मक दिशा में प्रवणता 10−3" T सेमी"^(-1)है(अर्थातऋणात्मकX−दिशामेंइकाईसेंटीमीटरदुरीपरक्षेत्रकेमानमें10^(-3) T सेमी−1 की वृद्धि होती है ) तथा क्षेत्र के मान में 10−3" T से"^(-1)कीदरसेकमीभीहोरहीहै।तथाक्षेत्रकेमानमेंसेमीकीदरसेकमीभीहोरहीहै।यदिकुंडलीकाप्रतिरोध4.50 m Omega हो , तो प्रेरित धारा का परिणाम एवं दिशा ज्ञात कीजिए।
View Solutionकोई रेखा x-अक्ष और y-से साथ क्रमशः 60∘ तथा 45∘ के कोण बनाती है। इनके द्वारा घनत्व दिशा में z-अक्ष के साथ कितना कोण बनेगा ?
View Solutionयह ज्ञात है की महाविद्यालय के छात्रों में से 60 % छात्रावास में रहते है और 40 % छात्रावास में नहीं रहते है । पूर्ववर्ती वर्ष से परिणाम सूचित करते है की छात्रावास में रहने वाले छात्रों में से30 % छात्रों में से 20 % छात्रों ने A ग्रेड लिए। वर्ष के अंत में महाविद्यालय के एक छात्र को यादृच्छया चुना गया और पाया गया की उसे A ग्रेड मिला है । इस बात की क्या प्रायिकता है की वह छात्रावास में रहने वाला है ?
View Solutionघर्षण किस दिशा में लगता है -
View Solutionएक व्यक्ति पश्चिम दिशा की ओर मूँह करके खड़ा है | वह दक्षिणावर्त दिशा में 45∘ के कोण पर घूमता है फिर वह पुनः उसी दिशा में 180∘ के कोण पर घूमता है और फिर वह वामावर्त दिशा में 270∘ के कोण पर घूमता है | अब वह किस दिशा की ओर खड़ा है ?
View Solutionप्रश्न|सामान दिशा में गति के लिये|विपरित दिशा में गति के लिये|OMR|Summary
View Solutionयदि P, Q के उत्तर दिशा में तथा R,P के दक्षिण-पश्चिम में तथा S, Q के उत्तर-पूर्व में है, तो इनमे से कौन-सा निश्चित रूप से सत्य है?
View Solutionवायु के आधिक्य में सोडियम के दहन से एक उच्च ऑक्साइड प्राप्त होता है । उत्पाद में ऑक्सीजन की ऑक्सीकरण अवस्था क्या है ? ऋणात्मक चिन्ह की उपेक्षा कीजिए ।
View Solutionकिस अभिक्रिया में, हाइड्रोजन परॉक्साइड न तो ऑक्सीकारक और न ही अपचायक के रूप में कार्य करता है?
View SolutionX और Y अणुओं के संबंध में निम्नलिखित कथनों में से कौन सा गलत है?
View Solutionप्रथम कोटि अभिक्रिया के लिए निम्नलिखित में से कौन सा सही है/हैं? (a अभिकारक की प्रारंभिक सांद्रता है, x अभिकृत अभिकारक की सांद्रता है और t समय है)
View Solutionयदि Mn2+ में अयुग्मित इलेक्ट्रॉनों की संख्या 'X' है और +2 की तुलना में अन्य धनात्मक ऑक्सीकरण अवस्था 'Y' है। यहाँ x + Y का योग क्या है|
View Solutionएक आदर्श गैस के दस मोलों को एक बंद पात्र में भरा जाता है । पात्र में बेलन और पिस्टन के प्रकार की व्यवस्था है और 0.821 atm पर गैस का दाब स्थिर रहता है। निम्नलिखित में से कौन सा आलेख logV और logT के परिवर्तन का सही निरूपण करता है? (V= आयतन(लीटर में) और T= ताप (केलिवन में)
View Solution
