R व्यासार्ध की एक लम्बी परिनालिका की प्रति यूनिट लम्बाई में n फेरे हैं और इसमें से समय के साथ परिवर्तित होने वाले ज्यावक्रीय धारा I=I0cosωt बहती है जहाँ I0, अधिकतम धारा है और ω, धारा स्रोत की कोणीय आवृत्ति।
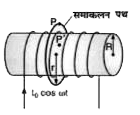
(a) परिनालिका से बाहर इसके अक्ष से r दूरी पर वैद्युत क्षेत्र निकालें।
(b) परिनालिका के अन्दर अक्ष से r दूरी पर कितना वैद्युत क्षेत्र है?
(a) P (बाह्य बिन्दु) पर वैद्युत क्षेत्र निकालने के लिए आइए हम r व्यासार्ध का परिनालिका पर केन्द्रित एक वृत्त लें जो रेखीय समाकलन का पथ है। क्योंकि
ϕB=BA=(μ0nI)πR2=μ0n(I0cosωt)πR2, इसलिए
dϕBdt=μ0nI0(−sinωt)ωπR2 ...(i)
=−πμ0nI0ωR2sinωt
फिर ∮→E.→dl=E(2πr) ...(ii)
क्योंकि ∮→E.→dl=−dϕBdt (फैराडे का व्यापक नियम), इसलिए
E(2πr)=πμ0nI0ωR2sinωt [समीकरण (i) और (ii) से]
या E=μ0nI0ωR22rsinωt (क्योंकि r>R)
यहाँ वैद्युत क्षेत्र समय के साथ ज्यावक्रीय रूप से बदलता है और इसका आयाम, परिनालिका से बाहर 1/r के अनुसार कम होता जाता है।
(b) आन्तरिक बिन्दु P. के लिए r<R और इसलिए
E(2πr)=πμ0nI0ωr2sinωt
या E=μ0nI0ω2rsinωt
यह दर्शाता है कि परिनालिका के अन्दर वैद्युत क्षेत्र का आयाम, r के साथ रैखिक रूप से बढ़ता है और समय के साथ ज्यावक्रीय रूप से परिवर्तित होता है।
Topper's Solved these Questions
- BOOK - GRB PUBLICATION HINDICHAPTER - वैद्युतचुम्बकीय प्रेरण EXERCISE - प्रश्नोत्तरी : 1 अंक26videos
वैद्युतचुम्बकीय प्रेरण
- BOOK - GRB PUBLICATION HINDICHAPTER - वैद्युतचुम्बकीय प्रेरण EXERCISE - प्रश्नोत्तरी : 2 और 3 अंक16videos
वैद्युतचुम्बकीय प्रेरण
- BOOK - GRB PUBLICATION HINDICHAPTER - वैद्युतचुम्बकीय प्रेरण EXERCISE - विषय-आधारित समस्याएँ : हल सहित (विविध प्रश्न)2videos
वैद्युतचुम्बकीय प्रेरण
- BOOK - GRB PUBLICATION HINDICHAPTER - वैद्युतचुम्बकीय तरंगे EXERCISE - प्रतियोगिता साम्रगी रिक्त स्थान भरना10videos
वैद्युतचुम्बकीय तरंगे
- BOOK - GRB PUBLICATION HINDICHAPTER - वैधुत आवेश EXERCISE - विषय-आधारित अभ्यास24videos
वैधुत आवेश
Similar Questions
चित्र में एक लम्बवत एकसमान चुम्बकीय क्षेत्र में लूप PQR की दो स्थितियाँ दिखाई गयी हैं। कुण्डली की किस स्थिति में प्रेरित विद्युत वाहक बल उत्पन्न होता है?
05:04View Solutionविद्युतचुम्बकीय प्रेरण के फैराडे के नियम बताएँ। उन्हें गणितीय रूप से व्यक्त करें।
02:55View Solutionएक लम्बी पतली परिनालिका में प्रति मीटर 400 फेरे हैं और इसका व्यासार्ध 1.1 cm है। परिनालिका में धारा एकसमान दर dI/dt से बढ़ रही है। परिनालिका के केन्द्र के निकट और अक्ष से 3.5 cm की दूरी पर प्रेरित वैद्युत क्षेत्र 8×10−6V/m है। dI/dt निकालें।
02:06View Solutionकिसी वैद्युतचुम्बकीय तरंग में आयाम E0 और B0 ___ होते हैं परन्तु मैक्सवेल के समीकरण के अनुसार ___ द्वारा सम्बन्धित होते हैं।
02:55View Solutionएक वस्तु पर −1.00×10−10C का नेट आवेश है। इसमें कितने अतिरिक्त इलेक्ट्रॉन है ?
04:06View Solutionएक श्रेणी LCR परिपथ में L=10.0H,C=40μF तथा R=60Omega को 240V वोल्ट के परिवर्ती आवृत्ति के प्रत्यावर्ती धारा स्त्रोत से जोड़ा गया है । गणना कीजिए -(i ) स्त्रोत की कोणीय आवृत्ति जो परिपथ को अनुनाद की अवस्था में लाती है ,(ii ) अनुनादी आवृत्ति पर धारा , (iii ) प्रेरक के सिरों के बीच अनुनाद की दशा में वर्ग - माध्य - मूल विभव पतन ।
02:29View Solutionनिम्नलिखित स्थितियों में एक चर बिंदु का बिन्दुपथ ज्ञात कीजिए जिसकी
y- अक्ष से दूरी , उसकी मूलबिंदु से दूरी की आधी है ।04:06View Solutionउस बिंदु का बिन्दुपथ ज्ञात कीजिए
जिसकी x-अक्ष से दूरी उसकी y-अक्ष से दूरी की तीन गुनी है ।02:42View Solutionउस बिंदु का बिन्दुपथ जिसकी y-अक्ष से दूरी , उसकी मूलबिंदु से दूरी की आधी है ………… होगा ।
08:10View Solutionएक वायु सेना का जहाज 100 किमी/घण्टा की दर से ऊर्ध्वाधरतः ऊपर की और चढ़ रहा है। यदि पृथ्वी की त्रिज्या r किमी है , तब इसके उड़ना शुरू के मिनट बाद जहाज से दिखाई देने वाले पृथ्वी का क्षेत्रफल A=2πr2hr+h जहाँ , h जहाज की पृथ्वी से दूरी है )
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
55:31View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
42:52View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
07:31View Solutionएक द्विध्रुव 10 सेमी लम्बा तथा आवेश 500μC से बना है। इसके अक्ष से 25 सेमी दूरी पर विद्युत क्षेत्र की तीव्रता होगी
04:53View Solutionनिम्नलिखित कॉलम को सुमेलित कीजिये
कॉलम-I कॉलम-II(A) एक समान आवेशित परावैधुत वलय(p) निकाय के बाहर नियत स्थिर विधुत क्षेत्र है(B) एक सामान आवेशित परावैधुत वलय कोणीय वेग ωसे घूर्णित है (q)चुम्बकीय क्षेत्र की तीव्रता(C) वलय में नियत धारा i(r)वैधुत क्षेत्र (प्रेरित)(D)i=i0cosωt(s) चुम्बकीय द्वि - ध्रुव आघूर्णView Solutionएक बिंदु की एक रेखा से दूरी|दो समान्तर रेखाओं के बीच की दूरी
51:40View Solution