Question

0.3cm व्यासार्ध का एक वृत्ताकार लूप, 20cm व्यासार्ध के कहीं बड़े वृत्ताकार लूप के समान्तर है। छोटे लूप का केन्द्र, बड़े लूप के अक्ष पर है। उनके केन्द्रों के बीच दूरी 15cm है। (a) दोनों लूपों का पारस्परिक प्रेरकत्व निकालें। (b) यदि 2.0A की धारा छोटे लूप में बहे, तो बड़े लूप से सम्बद्ध फ्लक्स कितना होगा?

Explanation

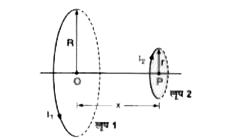
(a) यहाँ R (बड़े लूप अर्थात लूप 1 का व्यासार्ध)
`=20cm=0.2m`
दोनों लूपों के केन्द्रों के बीच दूरी `x=15cm=0.15m`
छोटे लूप में बहती धारा `I_(2)=2.0A`
यदि बड़े लूप में बहती धारा `I_(1)` हो, तो P पर इस लूप के कारण चुम्बकीय क्षेत्र
`B=(mu_(0)NI_(1)R^(2))/(2(R^(2)+x^(2))^(3//2))`
मान लें कि लूप 1 में बहती धारा `I_(1)` के कारण लूप 2 से सम्बद्ध फ्लक्स `phi_(21)` है।
स्पष्टतया, `phi_(21)=Bxx` लूप 2 का क्षेत्रफल अर्थात
`phi_(21) =(mu_(0)NI_(1)R^(2))/(2(R^(2)+x^(2))^(3//2))xxpi r^(2)" " ...(i)`
यदि लूप 2 का `I_(1)` धारा वाले लूप 1 से पारस्परिक प्रेरकत्व `M_(21)` हो, तो
`phi_(21)=M_(21)I_(1)" "...(ii)`
समीकरण (i) और (ii) से
`M_(21)I_(1)=(mu_(0)pi NI_(1)R^(2)r^(2))/(2(R^(2)+x^(2))^(3//2))`
या `M_(21)=(mu_(0)pi NR^(2)r^(2))/(2(R^(2)+x^(2))^(3//2))`
या `M_(21)=((4pi xx 10^(-7)) pi (0.2)^(2)(0.003)^(2))/(2[(0.2)^(2)+(0.15)^(2)]^(3//2))H`
(क्योंकि N = 1)
या `M_(21)=4.55xx10^(-11)H`
(b) यदि लूप 1 का लूप 2 से पारस्परिक प्रेरकत्व `M_(12)` हो, तो पारस्परिकता प्रमेय से
`M_(12)=M_(21)`
लूप 2 में धारा से लूप 1 से सम्बद्ध फ्लक्स
`phi_(12)=M_(12)I_(2)=(4.55xx10^(-11)H)(2A)=9.10xx10^(-11)Wb`