Establish the relationship between temperature pressure and volume of a given mass of a gas.
To establish the relationship between temperature, pressure, and volume of a given mass of gas, we can derive the ideal gas equation using three fundamental gas laws: Charles' Law, Boyle's Law, and Avogadro's Law. Here’s a step-by-step solution:
Step 1: Understand the Basic Gas Laws
1. Charles' Law states that the volume (V) of a gas is directly proportional to its temperature (T) when pressure (P) is held constant. Mathematically, this can be expressed as:
V∝T(P constant)
or
VT=k1(k1 is a constant)
2. Boyle's Law states that the volume (V) of a gas is inversely proportional to its pressure (P) when temperature (T) is held constant. This can be expressed as:
V∝1P(T constant)
or
PV=k2(k2 is a constant)
3. Avogadro's Law states that the volume (V) of a gas is directly proportional to the number of moles (n) of the gas when pressure and temperature are constant. This can be expressed as:
V∝n(P and T constant)
or
Vn=k3(k3 is a constant)
Step 2: Combine the Gas Laws
From the three laws, we can combine them to establish a relationship that includes temperature, pressure, and volume:
V∝nTandV∝1P
This leads us to:
V∝nTP
Step 3: Introduce the Gas Constant
To eliminate the proportionality, we introduce a constant (R), known as the gas constant:
V=nRTP
Step 4: Rearranging the Equation
Multiplying both sides by P gives us the ideal gas equation:
PV=nRT
Where:
- P = pressure of the gas
- V = volume of the gas
- n = number of moles of the gas
- R = ideal gas constant
- T = temperature of the gas in Kelvin
Step 5: Expressing in Terms of Given Mass
If we want to express the equation in terms of the mass of the gas, we can relate the number of moles (n) to the mass (m) and the molar mass (M) of the gas:
n=mM
Substituting this into the ideal gas equation gives:
PV=mMRT
Final Relationship
Thus, the relationship between temperature, pressure, and volume of a given mass of gas can be summarized as:
PV=nRTorPV=mMRT
1. Charles' Law states that the volume (V) of a gas is directly proportional to its temperature (T) when pressure (P) is held constant. Mathematically, this can be expressed as:
V∝T(P constant)
or
VT=k1(k1 is a constant)
V∝1P(T constant)
or
PV=k2(k2 is a constant)
V∝n(P and T constant)
or
Vn=k3(k3 is a constant)
From the three laws, we can combine them to establish a relationship that includes temperature, pressure, and volume:
V∝nTandV∝1P
This leads us to:
V∝nTP
To eliminate the proportionality, we introduce a constant (R), known as the gas constant:
V=nRTP
Multiplying both sides by P gives us the ideal gas equation:
PV=nRT
Where:
- P = pressure of the gas
- V = volume of the gas
- n = number of moles of the gas
- R = ideal gas constant
- T = temperature of the gas in Kelvin
If we want to express the equation in terms of the mass of the gas, we can relate the number of moles (n) to the mass (m) and the molar mass (M) of the gas:
n=mM
Substituting this into the ideal gas equation gives:
PV=mMRT
Thus, the relationship between temperature, pressure, and volume of a given mass of gas can be summarized as:
PV=nRTorPV=mMRT
Topper's Solved these Questions
- STATES OF MATTER : GASES AND LIQUIDSBook:MODERN PUBLICATIONChapter:STATES OF MATTER : GASES AND LIQUIDSExercise:Revision Exercises (Objective Questions)(Long Answer Questions)
Explore 8 Videos
- STATES OF MATTER : GASES AND LIQUIDSBook:MODERN PUBLICATIONChapter:STATES OF MATTER : GASES AND LIQUIDSExercise:Revision Exercises (Objective Questions)(Numerical Problems)
Explore 13 Videos
- STATES OF MATTER : GASES AND LIQUIDSBook:MODERN PUBLICATIONChapter:STATES OF MATTER : GASES AND LIQUIDSExercise:Revision Exercises (Objective Questions)(Very Short Answer Questions)
Explore 30 Videos
- SOME BASIC CONCEPTS OF CHEMISTRY Book:MODERN PUBLICATIONChapter:SOME BASIC CONCEPTS OF CHEMISTRY Exercise:COMPETITION FILE (INTEGER TYPE AND NUMERICAL VALUE TYPE QUESTIONS)
Explore 10 Videos
- STRUCTURE OF ATOMBook:MODERN PUBLICATIONChapter:STRUCTURE OF ATOMExercise:Unit Practice Test
Explore 13 Videos
Similar Questions
Knowledge Check
Two different isotherms representing the relationship between pressure p and volume V at a given temperature of the same ideal gas are shown for masses m1 and m2 then
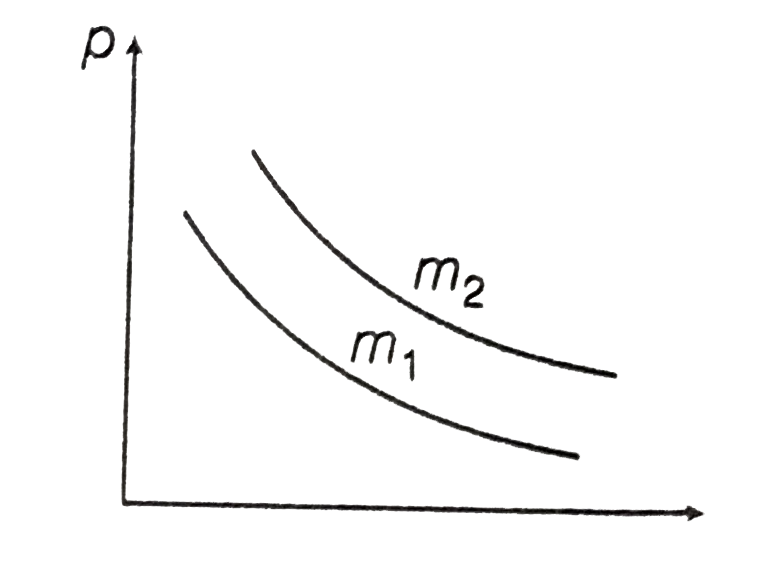 Am1>m2Bm1=m2Cm1<m2DNothing can be predicted
Am1>m2Bm1=m2Cm1<m2DNothing can be predictedAt constant temperature the product of pressure and volume of a given amount of a gas is constant. Ths is :
AGay -Lussac's lawBCharles' lawCBoyle's lawDpressure lawAt a given volume and temperature the pressure of a gas
Avaries inversely as its massBvaries inversely as the square of its massCvaries linearly as its massDis independent of its mass
Given the relationship between the molar volume of a gas and its molar mass.
View SolutionThe graph between pressure P and volume V for a given mass of a gas a fixed temperature T is a ________ .
View SolutionDerive the relationship between pressure, temperature and density of a gas (i.e. M=d RT/P).
View SolutionThe equation which describes the quantitative relationship between the pressure and the amount of gas adsorbed at constant temperature is known as
View SolutionAt a given volume and temperature the pressure of a gas
View Solution

