A solid sphere of density with one -third of tis volume submerged . When the sphere is pressed down slightly and released , it executes S.H.M of time period T. Then (viscous effect is ignored)
The correct Answer is:B, C
To solve the problem of a solid sphere of density σ with one-third of its volume submerged, executing simple harmonic motion (SHM) when pressed down and released, we will follow these steps:
Step 1: Determine the mass of the sphere
The volume V of a solid sphere is given by:
V=43πr3
The mass m of the sphere can be calculated using the formula:
m=V⋅σ=43πr3⋅σ
Step 2: Calculate the volume submerged in the liquid
Since one-third of the sphere's volume is submerged, the volume Vs submerged is:
Vs=13V=13⋅43πr3=49πr3
Step 3: Calculate the buoyant force acting on the sphere
The buoyant force Fb acting on the sphere is equal to the weight of the liquid displaced, which can be calculated as:
Fb=Vs⋅ρ⋅g=49πr3⋅ρ⋅g
where ρ is the density of the liquid.
Step 4: Establish the relationship between densities
For the sphere to float, the buoyant force must equal the weight of the sphere:
Fb=m⋅g
Substituting the expressions we have:
49πr3⋅ρ⋅g=43πr3⋅σ⋅g
Cancelling common terms gives:
49ρ=43σ
From this, we can derive:
ρ=3σ
Step 5: Determine the restoring force when the sphere is displaced
When the sphere is pressed down by a distance x, the volume of liquid displaced is:
Vd=A⋅x
where A is the cross-sectional area of the sphere at the water surface, given by:
A=πr2
Thus, the volume displaced is:
Vd=πr2x
The buoyant force when displaced is:
F′b=Vd⋅ρ⋅g=πr2x⋅(3σ)⋅g
The restoring force F acting on the sphere is:
F=−F′b=−πr2x⋅(3σ)⋅g
Step 6: Relate the restoring force to acceleration
Using Newton's second law, F=ma:
−πr2x⋅(3σ)⋅g=m⋅a
Substituting m=43πr3σ:
−πr2x⋅(3σ)⋅g=(43πr3σ)a
Cancelling πσ from both sides:
−3r2gx=43r3a
Thus,
a=−9g4rx
Step 7: Determine the angular frequency and time period
The equation for SHM is a=−ω2x, where:
ω2=9g4r
Taking the square root gives:
ω=32√gr
The time period T of SHM is given by:
T=2πω=2π32√gr=4π3√rg
Final Result
The time period T of the simple harmonic motion of the sphere is:
T=4π3√rg
The volume V of a solid sphere is given by:
V=43πr3
The mass m of the sphere can be calculated using the formula:
m=V⋅σ=43πr3⋅σ
Since one-third of the sphere's volume is submerged, the volume Vs submerged is:
Vs=13V=13⋅43πr3=49πr3
The buoyant force Fb acting on the sphere is equal to the weight of the liquid displaced, which can be calculated as:
Fb=Vs⋅ρ⋅g=49πr3⋅ρ⋅g
where ρ is the density of the liquid.
For the sphere to float, the buoyant force must equal the weight of the sphere:
Fb=m⋅g
Substituting the expressions we have:
49πr3⋅ρ⋅g=43πr3⋅σ⋅g
Cancelling common terms gives:
49ρ=43σ
From this, we can derive:
ρ=3σ
When the sphere is pressed down by a distance x, the volume of liquid displaced is:
Vd=A⋅x
where A is the cross-sectional area of the sphere at the water surface, given by:
A=πr2
Thus, the volume displaced is:
Vd=πr2x
The buoyant force when displaced is:
F′b=Vd⋅ρ⋅g=πr2x⋅(3σ)⋅g
The restoring force F acting on the sphere is:
F=−F′b=−πr2x⋅(3σ)⋅g
Using Newton's second law, F=ma:
−πr2x⋅(3σ)⋅g=m⋅a
Substituting m=43πr3σ:
−πr2x⋅(3σ)⋅g=(43πr3σ)a
Cancelling πσ from both sides:
−3r2gx=43r3a
Thus,
a=−9g4rx
The equation for SHM is a=−ω2x, where:
ω2=9g4r
Taking the square root gives:
ω=32√gr
The time period T of SHM is given by:
T=2πω=2π32√gr=4π3√rg
The time period T of the simple harmonic motion of the sphere is:
T=4π3√rg
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (Multiple choice question) based on a given passage/comprehension9videos
OSCILLATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (Matching Type Questions)2videos
OSCILLATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Competition File (JEE (Advanced) For IIT Entrance)7videos
OSCILLATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST16videos
MOTION IN A STRAIGHT LINE
- BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)6videos
PHYSICAL WORLD
Similar Questions
A tray of mass 12 kg is supported by two identical springs as shown in figure. When the tray is pressed down slightly and released, it executes SHM with a time period of 1.5s. What is the force constant of each spring?When a block of mass m is placed on the tray , the period of SHM changes to 3.0s. What is the mass of the block ?
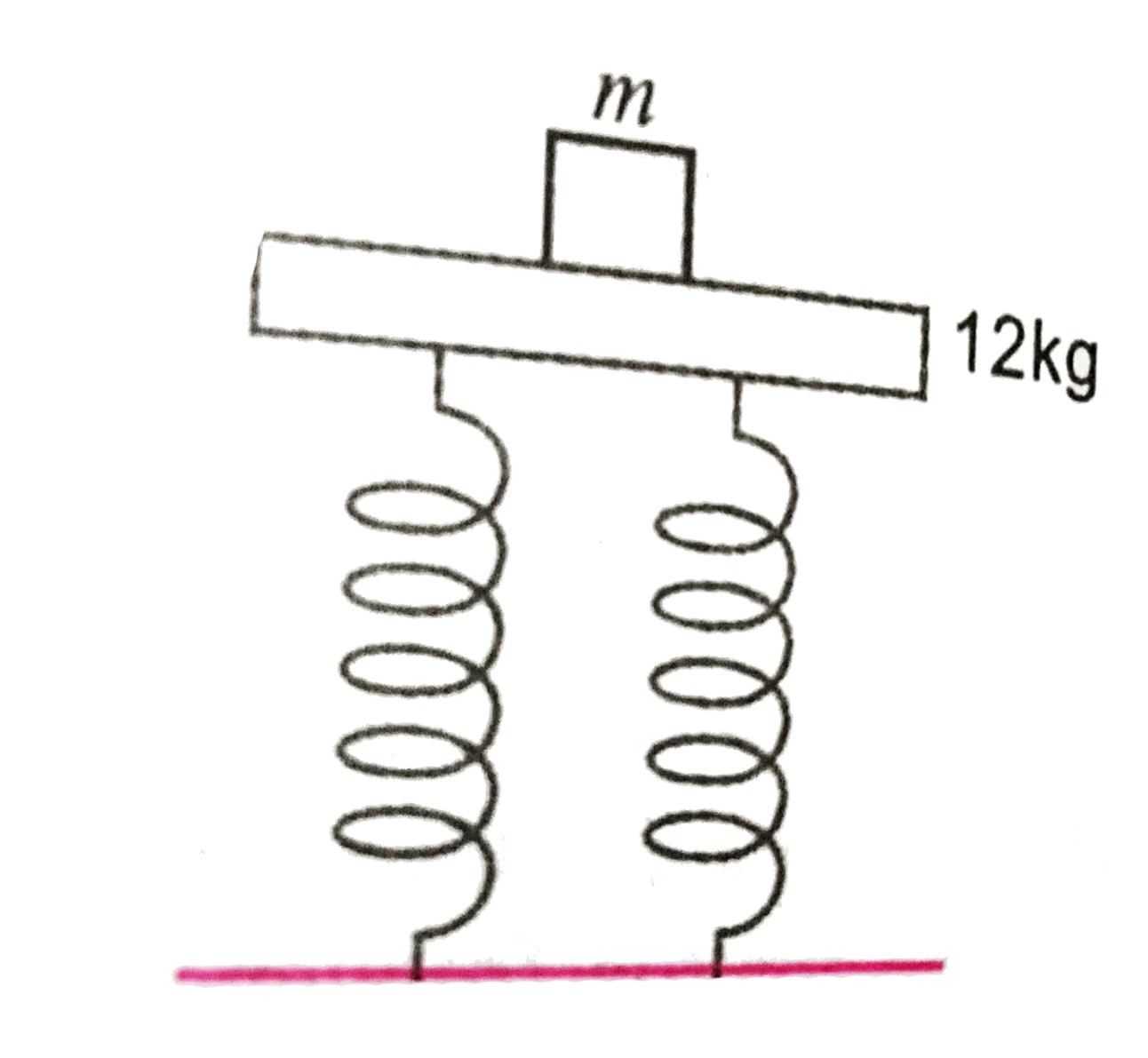 View Solution
View SolutionA solid sphere of radius R is floating in a liquid of density σ with half of its volume submerged. If the sphere is slightly pushed and released , it starts axecuting simple harmonic motion. Find the frequency of these oscillations.
View Solution
Knowledge Check
- Question 1 - Select One
A tunnel has been dug through the centre of the earth and a ball is released in it. It executes S.H.M. with time period
A42 minutesB1 dayC1 hourD84.6 minutes - Question 2 - Select One
A brass cube of side a and density σis floating in mercury of density ρ. If the cube is displaced a bit vertically, it executes S.H.M. Its time period will be
A2π√σaρgB2π√ρaσgC2π√ρgσaD2π√σgρa - Question 3 - Select One
A body of mass m is attached to the lower end of a spring whose upper end is fixed. The spring has negligible mass. When the mass m is slightly pulled down and released, it oscillates with a time period of 3s. When the mass m is increased by 1kg, the time period of oscillations becomes 5s. The value of m in kg is
A34B43C169D916
A tunnel has been dug through the centre of the earth and a ball is released in it. It executes S.H.M. with time period
View SolutionA vertical U tube contains a liquid of density ρ, length of the liquid in the tube is 2H. The liquid is displaced slightly and released. Show that the liquid will execute SHM. Also find its time period. Take liquid to be ideal.
 View Solution
View SolutionA small solid cylinder of mass M attached to horizontal massless spring can roll without slipping along a horizontal surface. Show that if the cylinder is displaced slightly and released, it executes S.H.M. Also find its time period.
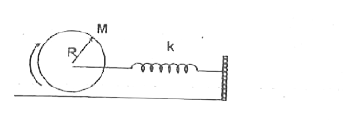 View Solution
View SolutionConsider a situation shown in the figure. Show that if the blocks are displaced slightly in opposite directions and released, they will execute S.H.M. calculate the time period.
 View Solution
View SolutionA body of mass m is attached to the lower end of a spring whose upper end is fixed. The spring has negligible mass. When the mass m is slightly pulled down and released, it oscillates with a time period of 3s. When the mass m is increased by 1kg, the time period of oscillations becomes 5s. The value of m in kg is
View Solution
