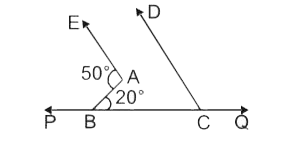
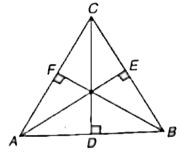
In the given triangle ABC,CD,BFandAE are the altitudes. If the ratio of CD:AE:BF=2:3:4, then the ratio of AB:BC:CA is :
A
4:3:2
B
2:3:4
C
4:9:16
D
6:4:3
Video Solution
Text Solution
The correct Answer is:D
|
Answer
Step by step video, text & image solution for In the given triangle ABC, CD, BF and AE are the altitudes. If the ratio of CD: AE : BF = 2:3:4, then the ratio of AB : BC: CA is : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 2)52videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.560videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 240videos
FUNDAMENTALS
- BOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions18videos
HCF AND LCM
Similar Questions
Knowledge Check
- Question 1 - Select One
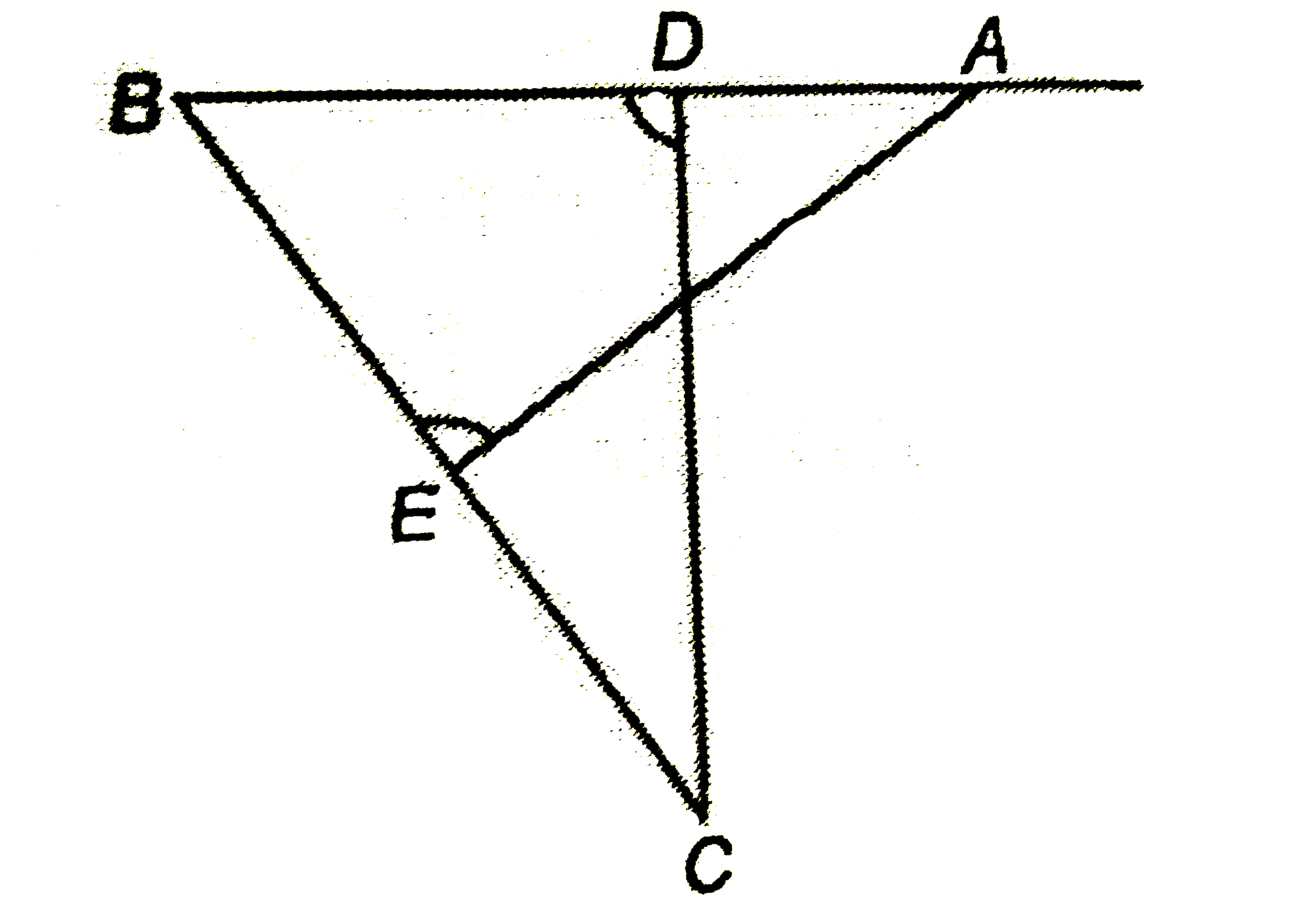
In the ajoining figure AE∣∣CD and BC∣∣ED, then find y:
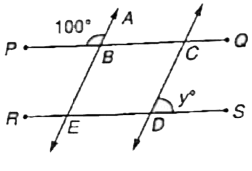 A60∘B80∘C90∘D75∘
A60∘B80∘C90∘D75∘ - Question 2 - Select One
ABC is a right-angled triangle, right angled at A and AD is the altitude on BC. If AB : AC= 3:4, what is the ratio BD:DC?
A3:4B9:16C2:3D1:2 - Question 3 - Select One
Let ABC be an acute angled triangle and CD be the altitude through C. If AB = 8 cm and CD = 6 cm, then the distance between the midpoints AD and BC is :
A6B4C4.5D5
In two triangles ABC and ADC, if AB=AD and BC=CD. Are they congruent?
View SolutionIn the given figure, ∠BDC=∠BEA and AB=BC. Show that AE=CD.
 View Solution
View SolutionIn the adjoining figure AE||CD and BC||ED, then find Y.
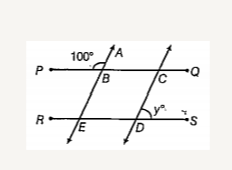 View Solution
View SolutionIn a triangle ABC, the altitude AD and the median AE divide ∠A into three equal parts. If BC=28, then the nearest integer to AB+ AC is
View SolutionIn the figure AB||CDandDE||BF. Find the valeu of x :
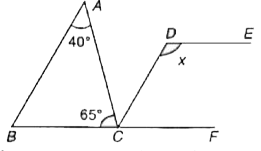 View Solution
View Solution