Let D be the mid-point of a straight line AB and let C be a point diff

Let X be the midpoint of the side AB of triangle ABC. And Y be the mid point of CX. If Z is the point where BY meets the side AC, then $A Z : Z C$ is equal to
A $1 : 1$
B $2 : 1$
C $3 : 1$
D $3 : 2$
If D id the mid-point of the side BC of a triangle ABC and AD is perpendicular to AC , then
A $a^{2} + b^{2} + c^{2} = 4 b^{2}$
B $a^{2} + b^{2} - c^{2} = 4 b^{2}$
C $a^{2} - b^{2} + c^{2} = 4 b^{2}$
D $a^{2} - b^{2} - c^{2} = 4 b^{2}$
Let ABCD be a trapezium in which AB||DC and E be the mid-point of AD. If F be a point on BC such that EF||AB. Then EF, where F is the mid-point of BC, is equal to

AAB + DC
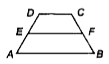B $\frac{1}{2} (A B + D C)$
C $\frac{1}{3} (A B + D C)$
DNone of these

Let D be the mid-point of a straight line AB and let C be a point different from D such that AC=BC, then.