Question

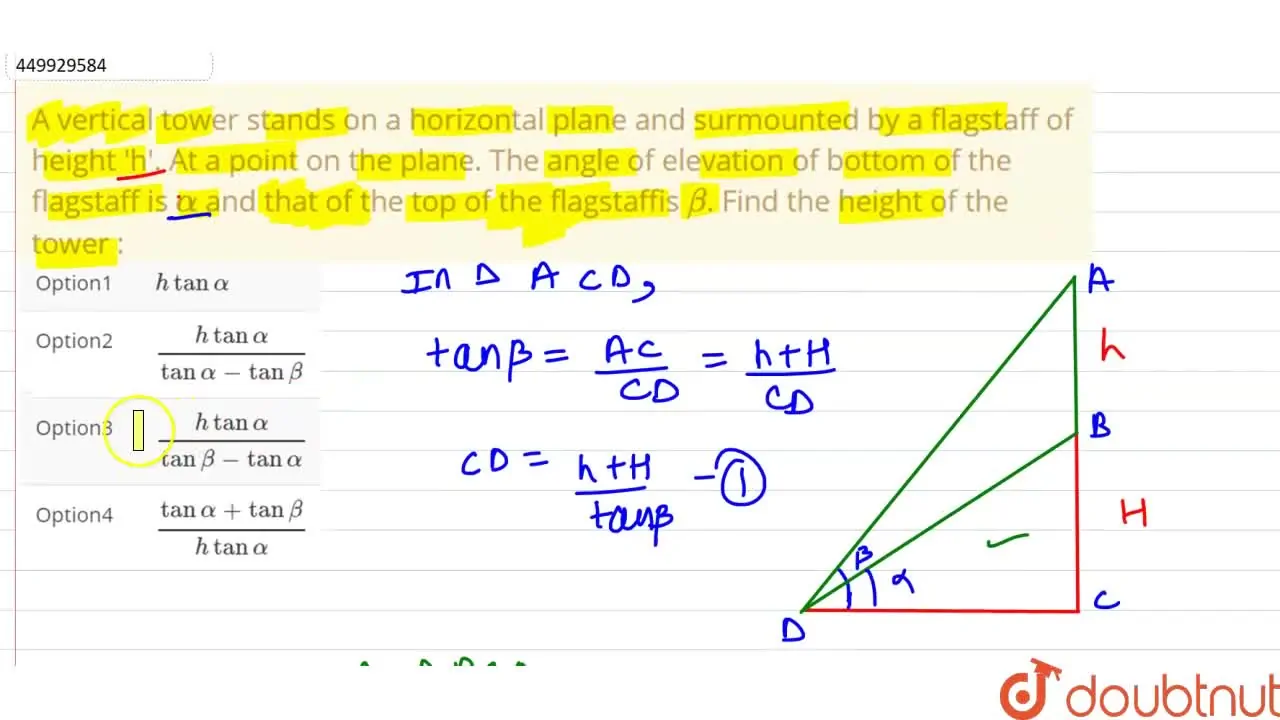
A vertical tower stands on a horizontal plane and surmounted by a flagstaff of height 'h'. At a point on the plane. The angle of elevation of bottom of the flagstaff is $\alpha$ and that of the top of the flagstaffis $\beta$. Find the height of the tower :

Options

A. `h tan alpha`
B. `(htanalpha)/(tanalpha-tan beta)`
C. `(htan alpha)/(tan beta-tan alpha)`
D. `(tanalpha+tanbeta)/(htan alpha)`

Answer

C

Explanation

To find the height of the tower (denoted as $$H$$) surmounted by a flagstaff of height $$h$$, we can use the information given about the angles of elevation from a point on the horizontal plane.

1. Understand the Setup:
- Let \( A \) be the point on the ground from where the angles are measured.
- Let \( B \) be the top of the flagstaff.
- Let \( C \) be the bottom of the flagstaff (which is on top of the tower).
- Let \( D \) be the ground level at the base of the tower.
- The height of the tower is \( H \) and the height of the flagstaff is \( h \).

2. Identify Angles:
- The angle of elevation to the bottom of the flagstaff (point \( C \)) is \( \alpha \).
- The angle of elevation to the top of the flagstaff (point \( B \)) is \( \beta \).

3. Use Trigonometric Ratios:
- From point \( A \) to point \( C \) (bottom of the flagstaff):
\( \tan(\alpha) = \frac{H}{d} \quad \text{(where \( d \) is the horizontal distance from point A to point D)}
\)
Rearranging gives:
\( d = \frac{H}{\tan(\alpha)} \quad \text{(Equation 1)} \)

- From point \( A \) to point \( B \) (top of the flagstaff):
\( \tan(\beta) = \frac{H + h}{d} \)
Rearranging gives:
\( d = \frac{H + h}{\tan(\beta)} \quad \text{(Equation 2)} \)

4. Equate the Two Expressions for \( d \):
- From Equation 1 and Equation 2:
\( \frac{H}{\tan(\alpha)} = \frac{H + h}{\tan(\beta)} \)

5. Cross-Multiply:
- Cross-multiplying gives:
\( H \cdot \tan(\beta) = (H + h) \cdot \tan(\alpha) \)

6. Expand and Rearrange:
- Expanding the right side:
\( H \cdot \tan(\beta) = H \cdot \tan(\alpha) + h \cdot \tan(\alpha) \)
- Rearranging gives:
\( H \cdot \tan(\beta) - H \cdot \tan(\alpha) = h \cdot \tan(\alpha) \)
- Factoring out \( H \):
\( H (\tan(\beta) - \tan(\alpha)) = h \cdot \tan(\alpha) \)

7. Solve for \( H \):
- Finally, solving for \( H \):
\( H = \frac{h \cdot \tan(\alpha)}{\tan(\beta) - \tan(\alpha)} \)

Final Result:
The height of the tower \( H \) is given by:
\( H = \frac{h \cdot \tan(\alpha)}{\tan(\beta) - \tan(\alpha)} \)