Find B and C of a triangle ABC, if b = 2 cm, c = 1 cm and A=60∘.
90∘and45∘
90∘and30∘
60∘and30∘
none of these
The correct Answer is:B
To find angles B and C of triangle ABC given that b=2cm, c=1cm, and A=60∘, we can use the cosine rule and the sine rule. Here’s a step-by-step solution:
Step 1: Use the Cosine Rule to find side a
The cosine rule states:
a2=b2+c2−2bc⋅cosA
Substituting the known values:
- b=2cm
- c=1cm
- A=60∘
We have:
a2=22+12−2⋅2⋅1⋅cos(60∘)
Calculating:
a2=4+1−2⋅2⋅1⋅12
a2=4+1−2
a2=3
a=√3cm
Step 2: Use the Cosine Rule to find angle B
Now, we can find angle B using the cosine rule again:
cosB=a2+c2−b22ac
Substituting the known values:
- a=√3
- b=2
- c=1
We have:
cosB=(√3)2+12−222⋅√3⋅1
cosB=3+1−42√3
cosB=02√3=0
Since cosB=0, we find:
B=90∘
Step 3: Use the Angle Sum Property to find angle C
We know that the sum of angles in a triangle is 180∘:
A+B+C=180∘
Substituting the known values:
60∘+90∘+C=180∘
C=180∘−150∘=30∘
Final Answer
Thus, the angles of triangle ABC are:
- B=90∘
- C=30∘
---
a2=b2+c2−2bc⋅cosA
- b=2cm
- c=1cm
- A=60∘
a2=22+12−2⋅2⋅1⋅cos(60∘)
a2=4+1−2⋅2⋅1⋅12
a2=4+1−2
a2=3
a=√3cm
cosB=a2+c2−b22ac
- a=√3
- b=2
- c=1
cosB=(√3)2+12−222⋅√3⋅1
cosB=3+1−42√3
cosB=02√3=0
B=90∘
A+B+C=180∘
Substituting the known values:
60∘+90∘+C=180∘
C=180∘−150∘=30∘
Thus, the angles of triangle ABC are:
- B=90∘
- C=30∘
Topper's Solved these Questions
- TRIGONOMETRYBook:ARIHANT SSCChapter:TRIGONOMETRYExercise:INTRODUCTORY EXERCISE - 11.6
Explore 10 Videos
- TRIGONOMETRYBook:ARIHANT SSCChapter:TRIGONOMETRYExercise:EXERCISE(LEVEL - 1)
Explore 35 Videos
- TRIGONOMETRYBook:ARIHANT SSCChapter:TRIGONOMETRYExercise:INTRODUCTORY EXERCISE - 11.4
Explore 8 Videos
- TIME, SPEED AND DISTANCEBook:ARIHANT SSCChapter:TIME, SPEED AND DISTANCEExercise:SPEED TEST (TSD)
Explore 10 Videos
- TRUE DISCOUNT AND BANKER'S DISCOUNTBook:ARIHANT SSCChapter:TRUE DISCOUNT AND BANKER'S DISCOUNTExercise:FAST TRACK PRACTICE
Explore 23 Videos
Similar Questions
Knowledge Check
In a triangle ABC, b = √3 cm, c = 1 cm, ∠A=30∘, what is the value of a ?
A√2 cmB2 cmC1 cmD12 cmWhat is the area of the triangle ABC with sides a = 10 cm, c=4 cm and angle B = 30∘?
A16cm2B12cm2C10cm2D8cm2If the angle A, B and C of a triangle ABC are in A.P and a:b=1: √3 If c=4 cm then the area (in sq. cm) of this triangle is :
A4√3B2√3C2√3D4√3
Construct a triangle ABC in which AB=2.2, BC=1.9 cm, and ∠B=54∘
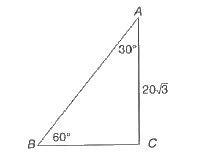
View SolutionFind side c of the triangle ABC , given that A=30∘,B=60∘ and b=20√3 .
View SolutionIf in a triangle ABC, a=1+√3cm,b=2cmand∠C=60∘ , then find the other two angles and the thire side
View SolutionIn ΔABC, if : a = 2 cm , b = 3cm and c = 4cm, then ∠A =
View SolutionIn a triangle ABC, if b+c=2aand∠A=60∘,then ΔABC is
View Solution
