द्विप्रिज्म क्या है ? इसके उपयोग से एकवर्णी प्रकाश का तरंग दैर्ध्य (λ) कैसे निकाला जाता है समझावें

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

व्यक्तिकरण प्रकाश तरंगो के अध्यारोपण की घटना है। इसकी निम्नलिखित है - (i) प्रकाश एकवर्णी होना चाहिए (ii) कम्पन विस्तार समान होना चाहिए (iii) प्रकाश स्त्रोत कला - सम्बद्ध होना चाहिए तथा (iv) को संकीर्ण होना चाहिए।
व्यक्तिकरण की घटना को प्रदर्शित करने के लिए फ्रेसनेल ने द्विक - प्रिज्म का प्रयोग किया। इसकी मदद से किसी प्राथमिक एकवर्णी प्रकाश - स्त्रोत के दो कला सम्बद्ध स्त्रोत प्राप्त किये जा सकते है यह दो प्रिज्मों के संयोग से बनता है जिनके अपवर्तक कोण काफी छोटे एक (लगभग 30 मिनट) होते है। इनके आधार एक दूसरे के संपर्क में रहते है इस कारण इनका एक कोण करीब 179∘ होता है।
जब इसको एकवर्णी प्रकाश स्त्रोत के समक्ष रखा जाता है तो अपवर्तन के बाद S1 तथा S2 से आती प्रतीत होती है। यानि S1 तथा S2 S का आभासी प्रतिबिम्ब है जो कला सम्बद्ध होते है अतः इनसे निर्गत प्रकाश तरंगो का अध्यारोपण होता है जिसके फलस्वरूप पर्दे पर व्यक्तिकरण। फ्रिन्जें प्राप्त होती है
पथान्तर =S2P−S1P
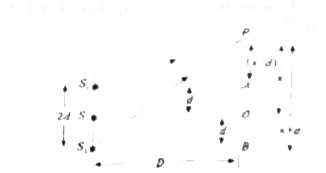
ocr_image
अब चित्र से, (S1P)2=D2+(x−d)2 तथा (S2P)2=D2+(x+d)2
अब (S2P)2−(S1P)2=(x+d)2−(x−d)2
या (S2P−S1P)(S2P+S1P)=x2+d2+2xd−x2−d2+2xd
या (S2P−S1P)4xd(SP+SP)
यदि OP काफी काम हो तो S1P=S2P=D अतः पथान्तर 4xdD+D=2xdD
ocr_image
संपोषी व्यक्तिकरण के लिए, पथान्तर =2xdD=nλ,x=nDλ2d
यदि n वें एवं (x+1) वें फ्रिन्ज की दूरी क्रमशः xn तथा xn+1 हो तो फ्रिन्ज की चौड़ाई
(β)=xn+1−xn(n+1)Dλ2d−nDλ2d=Dλ2dλ=2βdD
∴ यदि β, d एवं D मालूम हो तो λ का मान ज्ञात किया जा सकता है
इसी प्रकार विनाशी व्यक्तिकरण में भी λ=2βdD ही प्राप्त होता है
फ्रिन्ज की चौड़ाई का व्यंजक - समीकरण (i) की सहायता से ही संपोषी व्यक्तिकरण के β=Dλ2d लिए एवं विनाशी व्यक्तिकरण के लिए भी β=Dλ2d
यानी दीप्त एवं अदीप्त दोनों प्रकार की फ्रिन्जो की चौड़ाई समान होती।
यदि D = स्त्रोत की पर्दे से दूरी, λ= प्रक्षा तरंग का तरंगदैर्घ्य
2d= कला सम्बद्ध स्त्रोतों के बीच की दूरी, मालूम हो तो फ्रिन्ज की चौड़ाई ज्ञात जा सकती है।

Updated on:21/07/2023
|
Class 12PHYSICSQUESTION BANK

Topper's Solved these Questions

Similar Questions