What fraction of these circles have X’s in them?
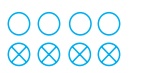
The correct Answer is:1/2
Let us understand this solution:
As we see that there are 8 circles, out of which 4 have X marked in them
the total number of circles = 8
Total number of circles having X = 4
Therefore, required fraction = number of circles with X / total number of circle = 4/8
Answer = 12.
Topper's Solved these Questions
Similar Questions
What fraction of these circles have X’s in them?

View SolutionFind the equation of the circle having centre in the first quadrant, touching the x-axis, having a common tangent y=√3x+4 with the circle x2+y2+4x+4y+4=0 such that the distance between the two circles along the x-axis is 3 units.
View Solution
Knowledge Check
The equation of the circle touching the lines |y| = x and having radius √2 is :
Ax2+y2+4x+2=0Bx2+y2−6x+7=0Cx2+y2−4x+2=0Dx2+y2−4x−3=0IF x2+y2−2y−15+λ(2x+y−9)=0 represents family of circles for. Different values of λ, then the equation of the circle(s) along these circles having minimum radius is/are
A3x2+3y2−2x−7y−36=0Bx2+y2−2y−15=0C5x2+5y2−32x−26y+69=0Dx2+y2−10x−7y+30=0
A circle x2+y2+4x−2√2y+c=0 is the director circle of circle S1andS2, is the director circle of circle S1, and so on. If the sum of radii of all these circles is 2, then find the value of c.
View SolutionThe equation of the circle having the lines x2+2xy+3x+6y=0 as its normals and having size just suffcient to contain the circle x(x−4)+y(y−3)=0 is
View SolutionAt x=A4, what fraction of the mechanical energy is potential ? What fraction is kinetic ? Assume potential energy to be zero at mean position.
View SolutionWhat fraction of the equilateral triangle shown below with three identical sectors of a circle is shaded?
View SolutionFind the equation of the circle having
centre at (7,-2) , and touching the X-axis
View SolutionA circle x2+y2+4x−2√2y+c=0 is the director circle of the circle S1andS1 is the director circle of circle S2, and so on. If the sum of radii of all these circles is 2, then the value of c is k√2 , where the value of k is___________
View Solution