The number of squares on a chessboards is :
102
108
216
204
The correct Answer is:D
To find the total number of squares on a chessboard, we need to consider squares of different dimensions that can fit within the 8x8 grid of the chessboard.
1. Understanding the Chessboard Dimensions:
A standard chessboard has 8 rows and 8 columns, making it an 8x8 grid.
2. Counting 1x1 Squares:
Each individual square on the chessboard is a 1x1 square. Since there are 8 rows and 8 columns, the total number of 1x1 squares is:
8×8=64
3. Counting 2x2 Squares:
A 2x2 square occupies 2 rows and 2 columns. The number of 2x2 squares that can fit horizontally and vertically is:
(8−1)×(8−1)=7×7=49
4. Counting 3x3 Squares:
Similarly, for 3x3 squares:
(8−2)×(8−2)=6×6=36
5. Counting 4x4 Squares:
For 4x4 squares:
(8−3)×(8−3)=5×5=25
6. Counting 5x5 Squares:
For 5x5 squares:
(8−4)×(8−4)=4×4=16
7. Counting 6x6 Squares:
For 6x6 squares:
(8−5)×(8−5)=3×3=9
8. Counting 7x7 Squares:
For 7x7 squares:
(8−6)×(8−6)=2×2=4
9. Counting 8x8 Squares:
Finally, for the 8x8 square (the entire chessboard):
(8−7)×(8−7)=1×1=1
10. Totaling All Squares:
Now, we add all the squares together:
64(1x1)+49(2x2)+36(3x3)+25(4x4)+16(5x5)+9(6x6)+4(7x7)+1(8x8)
=64+49+36+25+16+9+4+1=204
Final Answer:
The total number of squares on a chessboard is 204.
A standard chessboard has 8 rows and 8 columns, making it an 8x8 grid.
Each individual square on the chessboard is a 1x1 square. Since there are 8 rows and 8 columns, the total number of 1x1 squares is:
8×8=64
A 2x2 square occupies 2 rows and 2 columns. The number of 2x2 squares that can fit horizontally and vertically is:
(8−1)×(8−1)=7×7=49
Similarly, for 3x3 squares:
(8−2)×(8−2)=6×6=36
For 4x4 squares:
(8−3)×(8−3)=5×5=25
For 5x5 squares:
(8−4)×(8−4)=4×4=16
For 6x6 squares:
(8−5)×(8−5)=3×3=9
For 7x7 squares:
(8−6)×(8−6)=2×2=4
Finally, for the 8x8 square (the entire chessboard):
(8−7)×(8−7)=1×1=1
Now, we add all the squares together:
64(1x1)+49(2x2)+36(3x3)+25(4x4)+16(5x5)+9(6x6)+4(7x7)+1(8x8)
=64+49+36+25+16+9+4+1=204
The total number of squares on a chessboard is 204.
Topper's Solved these Questions
- PERMUTATIONS & COMBINATIONS Book:ARIHANT SSCChapter:PERMUTATIONS & COMBINATIONS Exercise:EXERCISE (LEVEL-2)
Explore 82 Videos
- PERMUTATIONS & COMBINATIONS Book:ARIHANT SSCChapter:PERMUTATIONS & COMBINATIONS Exercise:FINAL ROUND
Explore 38 Videos
- PERMUTATIONS & COMBINATIONS Book:ARIHANT SSCChapter:PERMUTATIONS & COMBINATIONS Exercise:INTRODUCTORY EXERCISE -(19.7 )
Explore 12 Videos
- PERCENTAGESBook:ARIHANT SSCChapter:PERCENTAGESExercise:Final round
Explore 50 Videos
- PERMUTATIONS AND COMBINATIONSBook:ARIHANT SSCChapter:PERMUTATIONS AND COMBINATIONSExercise:HIGHER SKILL LEVEL QUESTIONS
Explore 19 Videos
Similar Questions
The area of each square of a chessboard having 64 squares is 4cm2. If there is a border on all the sides of the chessboard of 2 cm, then the perimeter of the chessboard is:
64 वर्गों वाले एक शतरंज की बिसात के प्रत्येक वर्ग का क्षेत्रफल 4 वर्ग सेमी है | यदि इस बिसात की सभी भुजाओं पर 2 सेमी का किनारा है , तो इस शतरंज की बिसात का परिमाप ज्ञात करें |
View SolutionThe number of squares in the figure is :
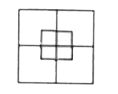
View Solution
Knowledge Check
The number of squares on a chessboards is :
A102B108C216D204The number of rectangles on a chess board is
A1008B1296C1124D1600The number of rectangles on a chess board is
A1008B1296C1124D1600
Find number of rectangles in a chessboard, which are not a square.
View SolutionWhat will be the number of unit squares on each side of a square graph paper if the total number of unit squares is 256?
View SolutionStatement-1: Number of rectangles on a chessboard is .8C2×.8C2.
Statement-2: To form a rectangle, we have to select any two of the horizontal lines and any two of the vertical lines.
View SolutionThree squares of a chessboard are chosen at random. the probability that two are of one colour and one of another is :
View SolutionThree squares of a chessboard are chosen at random. the probability that two are of one colour and one of another is :
View Solution