A cylinder with height and radius 2:1 is filled with soft drink and then it is titled so as to allow some soft drink to flow off to an extent where the level of soft drink just touches the lowest point of the upper mouth .
If the 2.1 L soft drink is retained in the cylinder , what is the capacity of the cylinder ?
3.6 L
4L
1.2 L
4.2 L
The correct Answer is:D
To solve the problem step by step, we need to understand the relationship between the volume of the cylinder and the amount of soft drink retained after it has been tilted.
Step 1: Understand the relationship between the volume retained and the total volume of the cylinder.
When the cylinder is tilted, the soft drink level touches the lowest point of the upper mouth. This means that the volume of soft drink retained in the cylinder is half of the total volume of the cylinder.
Step 2: Set up the equation based on the information given.
Let the total volume of the cylinder be V. According to the problem, the volume of soft drink retained in the cylinder is 2.1 liters. Since this volume is half of the total volume, we can write the equation:
V2=2.1 liters
Step 3: Solve for the total volume V.
To find the total volume V, we can multiply both sides of the equation by 2:
V=2×2.1=4.2 liters
Step 4: State the final answer.
The capacity of the cylinder is 4.2 liters.
Summary of the solution:
- The volume of soft drink retained is half of the total volume of the cylinder.
- The equation V2=2.1 liters leads us to find that the total volume V=4.2 liters.
When the cylinder is tilted, the soft drink level touches the lowest point of the upper mouth. This means that the volume of soft drink retained in the cylinder is half of the total volume of the cylinder.
Let the total volume of the cylinder be V. According to the problem, the volume of soft drink retained in the cylinder is 2.1 liters. Since this volume is half of the total volume, we can write the equation:
V2=2.1 liters
To find the total volume V, we can multiply both sides of the equation by 2:
V=2×2.1=4.2 liters
The capacity of the cylinder is 4.2 liters.
- The volume of soft drink retained is half of the total volume of the cylinder.
- The equation V2=2.1 liters leads us to find that the total volume V=4.2 liters.
Topper's Solved these Questions
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - TEST OF YOUR LEARNING
18 Videos
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - EXERCISE (LEVEL 1)
55 Videos
- LOGARITHM BOOK - ARIHANT SSCCHAPTER - LOGARITHM EXERCISE - EXERCISE LEVEL 2
19 Videos
- MIXED GRAPHBOOK - ARIHANT SSCCHAPTER - MIXED GRAPHEXERCISE - Higher Skill Level Questions
15 Videos
Similar Questions
A cylinder with height and radius 2:1 is filled with soft drink and then it is tilted so as to allow some soft drink to flow off to an extent where the level of soft drink just touches the lowest point of the upper mouth. If 2.1 L of soft drink is retained in the cylinder, what is the capacity of the cylinder ?
View SolutionFigure 8.2 shows a child blowing air with a straw near the opening of another straw which has its other end in a soft drink bottle. It was observed that the level of the soft drink in the straw rises up as soon as air is blown over its open end. Which one of the following best explains the reason for rise in level of the drink?

View Solution
Knowledge Check
A cylinder with height and radius 2:1 is filled with soft drink and then it is titled so as to allow some soft drink to flow off to an extent where the level of soft drink just touches the lowest point of the upper mouth .
If the 2.1 L soft drink is retained in the cylinder , what is the capacity of the cylinder ?A3.6 LB4 LC1.2 LD4.2 LA cylinder with height and radius 2:1 is filled with soft drink and then it is titled so as to allow some soft drink to flow off to an extent where the level of soft drink just touches the lowest point of the upper mouth .
If the quantity of soft drink left is poured into a conical flask whose heights and base radius are same as that of the cylinder so as to fill the conical flask completely , the quantity of soft drink left in the cylinder as a fraction of its total capacity is :A13B16C19D110A cylinder with height and radius 2:1 is filled with soft drink and then it is titled so as to allow some soft drink to flow off to an extent where the level of soft drink just touches the lowest point of the upper mouth .
If the quantity of soft drink left is poured into a conical flask whose heights and base radius are same as that of the cylinder so as to fill the conical flask completely , the quantity of soft drink left in the cylinder as a fraction of its total capacity is :A13B16C19D110
Ajay and Rakesh live in Rajgarh town of Churu districk of Rajasthan. As usual, the summer in this area of Rajasthan in extremely hot. Ajay's sister is getting engaged in the month of May, Ajay's family and relatives were waiting for the guests to arrive for the engagement ceremony. They had brought a slab of ice and put it in a tub of water for cooling the warm bottles of soft drinks. Just when they had finished drinking all the cold soft drink bottles, the gruests (including would-be bridegroom) arrive. Ajay and Rakesh were in a fix because they had only warm bottles of soft drinks left with them. Ajay suggested that they should put the warm soft drink bottles in the ice cold water which they already had in the tub but Rakesh did not agree with him Rakesh quickly brought a big slab of ice from the nearby shop crushed it well. He then put the warm soft drink bottles in an empty tub and surrounded them well with crushed ice. These warm soft drink bottles got colled in a short time and were served to the guests. All the guests enjoyed cold soft drinks on a very hot day and felt refreshed.
(a) What is the temperature of water formed from freshly melted ice ?
(b) What is the temperature of melting ice ?
(c) A person holds some ice-old water in his left hand palm and a piece of ice in his right hand palm. Which of the two will appear to be more cold and why ?
(d) Explain why, the warm drink bottles could be cooled more quickly by placing them in a tub of crushed ice than in a tub of ice cold water.
(e) Can you suggest another way in which the warm soft drinks can be cooled even more quickly by using ice (than by keeping the bottles in crushed ice) ?
(f) What type of change of state takes place when ice is used for cooling purposes ? What is the special name of this change of state ?
(g) What values are displayed by Rakesh in the episode ?
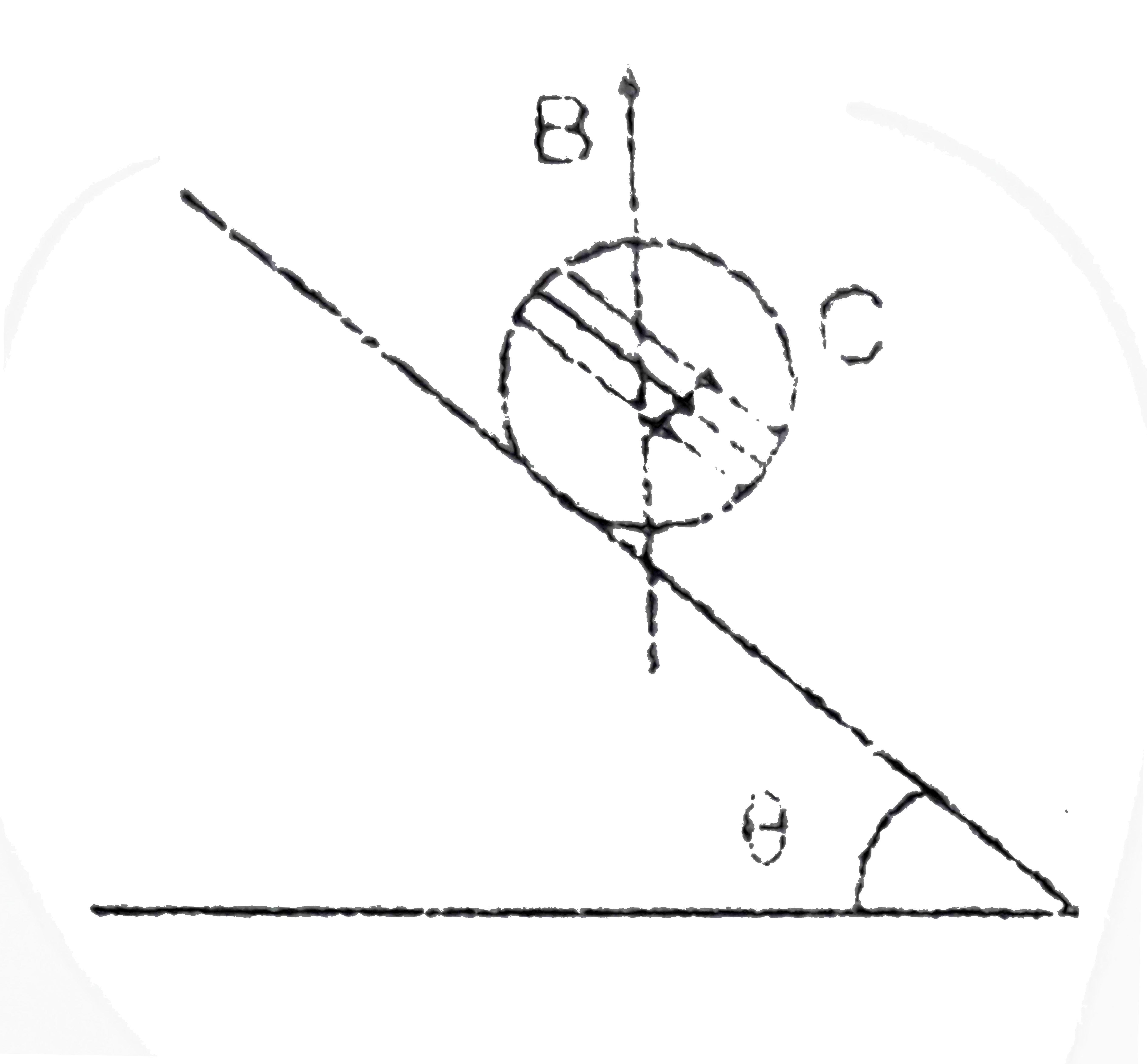
View SolutionFigure shows (only cross section) a wooden cylinder C with a mass m of 0.25kg,a radius R and a length l perpenducular to the plane of paper of 0.1meter with N=10 where N is number of turns of wire loop contains the axis of the cylinder the least current through the loop is P2A that will prevent the cylinder from moving down a plane whose surface is inclined at angle θ to the horizontal, in the presence of a vertical field of magnetic induction 0.5weber/meter2, if the planer of the windings is parallel to the inclinded plane?(bottom most point of cylinder does not slip)then find value of P.
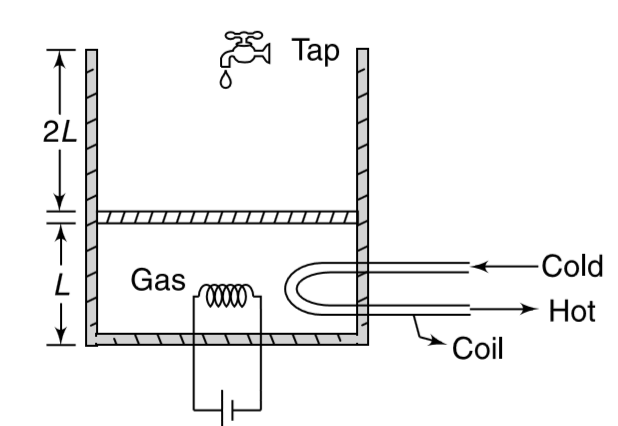
View SolutionA cylindrical container of height 3L and cross sectional area A is fitted with a smooth movable piston of negligible weight. It contains an ideal diatomic gas. Under normal atmospheric pressure P0 the piston stays in equilibrium at a height L above the base of the container. The gas chamber is provided with a heater and a copper coil through which a cold liquid can be circulated to extract heat from the gas. Volume occupied by the heater and the liquid coil is negligible. Following set of operations are performed to take the gas through a cyclic process.
(1) Heater is switched on. At the same time a tap above the cylinder is opened. Water fills slowly in the container above the piston and it is observed that the piston does not move. Water is allowed to fill the container so that the height of water column becomes L. Now the tap is closed.
(2) The heater is kept on and the piston slowly moves up. Heater is switched off at the time water is at brink of overflowing.
(3) Now the cold liquid is allowed to pass through the coil. The liquid extracts heat from the gas. Water is removed from the container so as to keep the position of piston fixed. Entire water is removed and the gas is brought back to atmospheric pressure.
(4) The circulation of cold liquid is continued and the piston slowly falls down to the original height L above the base of the container. Circulation of liquid is stopped. Assume that the container is made of adiabatic wall and density of water is ρ. Force on piston due to impact of falling water may be neglected.
(a) Draw the entire cycle on a P–V graph.
(b) Find the amount of heat supplied by the heater and the amount of heat extracted by the cold liquid from the gas during the complete cycle.
View SolutionA wooden cylinder of diameter 4 r, height H and density ρ/3 is kept on a hole of diameter 2 r of a tank, filled with water of density ρ as shown in the

If level of liquid starts decreasing slowly, when the level of liquid is at a height h1 above the cylinder, the block just start moving up. Then the value of h1 is
View SolutionThe Indian ceonomy is currently passing through a phase of relatively slow growth. However, this should not cloud the fact that over the nine-year period beginning 2005-06, the average annual growth rate was 7.7 per cent. Against this background, the relevant question is whether India has the capability to grow at 8 to 9 per cent in a sustaincd way. In short, what is the potential rate of growth of India?
Normally, potential growth is measured using trends with some filters. In one sense, these are backward-looking measures, since they depend on historically observed data. In the case of measuring capacity utilisation in manufacturing, the maximum capacity is very often taken as the maximum output achieved in the recent period. Perhaps, in the case of determining the potential rate of growth of the economy also, one can take the maximum growth rate achieved in the recent past as the lowest estimate of the potential. However, this assumption will be valid only if there is reason to believe that the maximum growth rate achieved in the recent past was not a one-off event and that the growth rate achieved was robust and replicable.
India achieved a growth rate of 9.5 per cent in 2005-06, followed by 9.6 per cent and 9.3 per cent in the subsequent two years. After declining a bit in the wake of international financial crisis, the growth rate went back to 8.9 per cent in 2010-11. In many ways the growth rate achieved in the high phase period of 2005-06 to 2007-08 was robust. The domestic savings rate during this period averaged 34.9 per cent of GDP. Similarly, the gross capital formation rate averaged 36.2 per cent. The current account deficit (CAD) remained low with an average of 1.2 per cent of GDP. Agricultural growth during this period averaged 5 per cent, and the annual manufacturing growth rate was 11 per cent. The capital flows were large but as the CAD remained low, the accretion to reserves amounted to $144 billion. Inflation during the period averaged 5.2 per cent. The combined fiscal deficit of the Centre and States was 5.2 per cent of GDP, well below the stipulated 6 per cent. Thus on many dimensions the growth rate was robust levels. Also, a booming external environment provided good support.
To assess whether the high growth phase can be replicated, we need to understand the factors that led to the slowdown since 2011-12. Complicating the analysis of this period is the revision of national income numbers with a new base. The two sets of numbers present a somewhat differing picture. According to the earlier series, the growth rate of the Indian economy fell below 5 per cent in 2012-13 and 2013-14. But the new serics shows a decline below 5 per cent only in 201213. For 2013- 14. the new series records a growth rate of 6.6 per cent, as against 4.7 per cent according to the earlier estimate. For 2014- 15 and 2015-16, there is only one set of numbers, that is, according to the new series. For both the years the growth rate is above 7 per cent. These are good growth rates under any circumstance, let alone the current global situation. Anyway. we have come down from the growth rate of 9-plus per cent which we had seen earlier.
Three sets ofC reasons are attributed for the slowdown. First the external environment had deteriorated sharply. The recovery from the crisis of 2008 was tepid. One country after another in the developed world came undcer pressure. Strangely, However, international commodity prices including crude oil prices remained high until a couple of years ago. All this had an adverse impact on developing countries, including India. However, it would be wrong to attribute the slowdown in India primarily to cxternal factors. The domestic factors are the key. Second, there were severe supply bottlenecks. Agricultural production fell sharply in 2009-10 because of a severe drought. This triggered an inflation which lasted for several years thereafter. Coal output fell. Iron ore output fell, partly because of court decisions. The third set of reasons is basically non- cconomic which led collectively to a weakening of investment. A multitude of issues relating to scams and perceived delays In decisionmaking created an element of uncertainty in the minds of investors. New investments began to fall.
The rise in investment rate must be supported by a rise in the domestic saving rate. An increase in investment rate supported by a widening current account deficit is not sustainable and is fraught with serious consequences. Only a current account deficit in the region of 1 to 1.5 per cent is sustainable. Incremental capital output ratio is a catch all variable which is influenced by a host of factors. Obviously it depends on technology. It also depends upon the skill of the labour force which in turn depends on the quality of the education system. Another catch-all expression "ease of doing business" is also relevant (i.e.) bureaucratic hurdles which impede speedy execution of projects need to be removed. Thus improving the productivity of capital needs action on several fronts. Making a prediction about the future is always hazardous. Many things can go wrong. The Indian economy in the recent past has shown that it has the resilience to grow at 8 to 9 per cent. Therefore achieving the required investment rate to support such a high growth is very much in the realm of possibility. However, we need to overcome the current phasc of declining investment rate. Investment sentiment is influcnced by non-economic factors as well. An environment of political and social cohesion is imperative. Equally, we can get the incremental capital- output ratio (ICOR) to a lower level. Raising the productivity of capital will require policy reforms including administrative reforms as well as firm-level improvements. The "potential" to grow at 8 to 9 per cent at least for a decade exists. We have to make it happen.
(The topic of the Passage asked in the exam was based on the economic changes in the last 50 years)
In context of the given passage, which of the following is/ are the reason for economic slowdown of India?
View Solution
