The base of a triangular field is three times its heigth. If the cost of cultivating the field is Rs. 36.72 per hectares is Rs. 495.72 , find the heigth and base of the triangular field :
480 m, 1120 m
400m, 1200 m
300 m , 900 m
250 m, 650 m
The correct Answer is:C
To solve the problem, we need to find the height and base of a triangular field given that the base is three times its height and the cost of cultivating the field is provided. Let's break down the solution step by step.
Step 1: Define Variables
Let the height of the triangular field be x meters. Since the base is three times the height, we can express the base as:
Base=3x meters
Step 2: Calculate the Area of the Triangle
The area A of a triangle is given by the formula:
A=12×Base×Height
Substituting the values we have:
A=12×(3x)×x=3x22 square meters
Step 3: Convert the Total Cost to Area
We know the total cost of cultivating the field is Rs. 495.72, and the cost per hectare is Rs. 36.72. To find the area in hectares, we can use the formula:
Area in hectares=Total CostCost per hectare=495.7236.72
Calculating this gives:
Area in hectares=13.5 hectares
Step 4: Convert Hectares to Square Meters
Since 1 hectare is equal to 10,000 square meters, we convert the area:
Area in square meters=13.5×10,000=135,000 square meters
Step 5: Set the Areas Equal
Now we can set the area calculated from the dimensions equal to the area calculated from the cost:
3x22=135,000
Step 6: Solve for x2
To eliminate the fraction, multiply both sides by 2:
3x2=270,000
Now, divide by 3:
x2=90,000
Step 7: Find x
Taking the square root of both sides gives:
x=√90,000=300 meters
Step 8: Calculate the Base
Now that we have the height, we can find the base:
Base=3x=3×300=900 meters
Final Answer
The height of the triangular field is 300 meters, and the base is 900 meters.
---
Let the height of the triangular field be x meters. Since the base is three times the height, we can express the base as:
Base=3x meters
The area A of a triangle is given by the formula:
A=12×Base×Height
Substituting the values we have:
A=12×(3x)×x=3x22 square meters
We know the total cost of cultivating the field is Rs. 495.72, and the cost per hectare is Rs. 36.72. To find the area in hectares, we can use the formula:
Area in hectares=Total CostCost per hectare=495.7236.72
Calculating this gives:
Area in hectares=13.5 hectares
Since 1 hectare is equal to 10,000 square meters, we convert the area:
Area in square meters=13.5×10,000=135,000 square meters
Now we can set the area calculated from the dimensions equal to the area calculated from the cost:
3x22=135,000
To eliminate the fraction, multiply both sides by 2:
3x2=270,000
Now, divide by 3:
x2=90,000
Taking the square root of both sides gives:
x=√90,000=300 meters
Now that we have the height, we can find the base:
Base=3x=3×300=900 meters
The height of the triangular field is 300 meters, and the base is 900 meters.
Topper's Solved these Questions
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - INTRODUCTORY EXERCISE- 10.3
15 Videos
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - INTRODUCTORY EXERCISE- 10.4
25 Videos
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - INTRODUCTORY EXERCISE- 10.1
32 Videos
- LOGARITHM BOOK - ARIHANT SSCCHAPTER - LOGARITHM EXERCISE - EXERCISE LEVEL 2
19 Videos
- MIXED GRAPHBOOK - ARIHANT SSCCHAPTER - MIXED GRAPHEXERCISE - Higher Skill Level Questions
15 Videos
Similar Questions
The adjacent sides of a parallelogram are 6 cm and 8 cm and the angle between them is 30∘ . What is the area of the parallelogram ?
View SolutionIf the circumference of a circle is 704 cm, then its area is :
View SolutionA rectangular field has its length and breadth in the ratio of 16 : 9. If its perimeter is 750 cm. What is its area?
View SolutionFind the sum of 'n' terms of the series.
log2(xy)+log4(xy)2+log8(xy)3+log16(xy)4 +……..
View SolutionDirections (Q. Nos. 1-5) The pie charts below show the percentage of students in each faculty at North- West University and the number of non- US students in the Arts faculty. These percentages have been rounded to the nearest whole number. There are a total 1049 students in Arts faculty. Use this information to answer the fallowing questions.
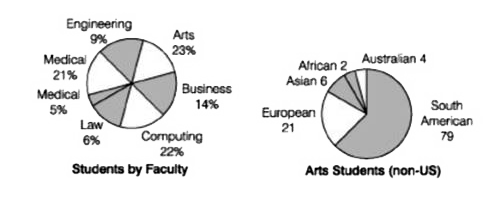
What percentage of students in the Arts faculty are non-US students?
View SolutionThe base of a triangular field is three xx its height and its area is 1350m^(2). Find the base and height of the field.
View SolutionThe base of a triangular field is three times its altitude. If the cost of cultivating the field at Rs 24.60 per hectare is Rs 332.10, find its base and height.
View SolutionThe base of a triangular field is three times its altitude . If the cost of sowing the field at Rs. 960 per hectare is Rs. 12960 , find its base and height .
View SolutionThe base of a triangular field is three times its altitude. If the cost of sowing the field at Rs. 58 per hectare is Rs. 783, Find its base and height.
View SolutionThe base of a triangular field is three times its height. If the cost of cultivating the field at Rs. 2800 per hectare is Rs.37800. find its base and height.
View SolutionThe base of a triangular field is three times its height. If the cost of cultivating the field at Rs.1080 per hectare is Rs.14580, find its base and height.
View SolutionThe altitude of a triangular field is one-third of its base. If the cost of showing the field at Rs.58 per hectare is Rs.783 then its altitude is
View Solutionकिसी त्रिभुजाकार क्षेत्र का आधार उसके शीर्षलंब का तीन गुना है। यदि इस क्षेत्र में 36.72 रू0 प्रति हेक्टयर की दर से बीज बनाने का खर्च 495.72 रू0 हो तो इस क्षेत्र का आधार एवं शीर्षलंब ज्ञात करें।
View SolutionThe base of a triangular field is three times its altitude. If the cost of cultivating the field at Rs 24.60 per hectare is Rs 332.10, find its base and height.
View Solutionएक त्रिभुजाकार खेत का आधार, इसके शीर्षलम्ब का तीन गुना है यदि खेत को 58 रुपए प्रति हेक्टेयर की दर से बोने का खर्च 783 रुपए हो, तो इसकी आधार और ऊंचाई ज्ञात करें ।
View Solution
