If the length of a rectangular field is doubled and its breadth is halved (i.e, reduced by 50% ) . What is percentage change in its area ?
The correct Answer is:A
To solve the problem, we need to calculate the percentage change in the area of a rectangular field when its length is doubled and its breadth is halved.
1. Define the Original Dimensions:
Let the original length of the rectangle be L and the original breadth be B.
2. Calculate the Original Area:
The area A of a rectangle is given by the formula:
A=Length×Breadth
Therefore, the original area Aoriginal is:
Aoriginal=L×B
3. Define the New Dimensions:
According to the problem, the length is doubled and the breadth is halved:
- New length Lnew=2L
- New breadth Bnew=B2
4. Calculate the New Area:
The new area Anew is:
Anew=Lnew×Bnew=(2L)×(B2)
Simplifying this gives:
Anew=2L×B2=L×B=Aoriginal
5. Calculate the Change in Area:
The change in area is:
Change in Area=Anew−Aoriginal=(L×B)−(L×B)=0
6. Calculate the Percentage Change in Area:
The percentage change in area is calculated using the formula:
Percentage Change=(Change in AreaAoriginal)×100
Substituting the values:
Percentage Change=(0L×B)×100=0%
Conclusion:
The percentage change in the area of the rectangular field is 0%.
Let the original length of the rectangle be L and the original breadth be B.
The area A of a rectangle is given by the formula:
A=Length×Breadth
Therefore, the original area Aoriginal is:
Aoriginal=L×B
According to the problem, the length is doubled and the breadth is halved:
- New length Lnew=2L
- New breadth Bnew=B2
The new area Anew is:
Anew=Lnew×Bnew=(2L)×(B2)
Simplifying this gives:
Anew=2L×B2=L×B=Aoriginal
The change in area is:
Change in Area=Anew−Aoriginal=(L×B)−(L×B)=0
The percentage change in area is calculated using the formula:
Percentage Change=(Change in AreaAoriginal)×100
Substituting the values:
Percentage Change=(0L×B)×100=0%
The percentage change in the area of the rectangular field is 0%.
Topper's Solved these Questions
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - INTRODUCTORY EXERCISE- 10.2
10 Videos
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - INTRODUCTORY EXERCISE- 10.3
15 Videos
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - TEST OF YOUR LEARNING
18 Videos
- LOGARITHM BOOK - ARIHANT SSCCHAPTER - LOGARITHM EXERCISE - EXERCISE LEVEL 2
19 Videos
- MIXED GRAPHBOOK - ARIHANT SSCCHAPTER - MIXED GRAPHEXERCISE - Higher Skill Level Questions
15 Videos
Similar Questions
What is the area of the triangle whose side are 84 m , 80 m and 52 m ?
View SolutionThe adjacent sides of a parallelogram are 6 cm and 8 cm and the angle between them is 30∘ . What is the area of the parallelogram ?
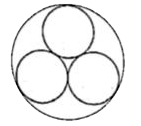
View SolutionThree equal circles each of radius 1 cm are circumscribed by a larger circle. Find the perimeter of the circumscribing circle :
View SolutionFind the sum of 'n' terms of the series.
log2(xy)+log4(xy)2+log8(xy)3+log16(xy)4 +……..
View SolutionDirections (Q. Nos. 1-5) The pie charts below show the percentage of students in each faculty at North- West University and the number of non- US students in the Arts faculty. These percentages have been rounded to the nearest whole number. There are a total 1049 students in Arts faculty. Use this information to answer the fallowing questions.
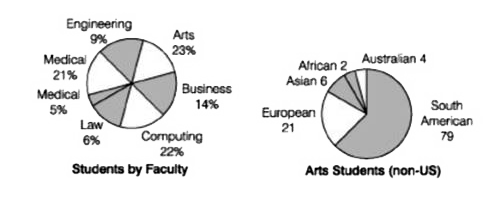
What percentage of students in the Arts faculty are non-US students?
View SolutionThe length of a rectangular field is 100m. If its perimeter is 300m, what is its breadth?
View SolutionWhat will happen to the area of a rectangle if its Length and breadth are trebled. Length is doubled and breadth is same. Length is doubled and breadth is halved.
View SolutionThe length of a rectangle is halved, while its breadth is tripled. What is the percentage change in area? 25% increase (b) 50% increase (c) 50% decrease (d) 75% decrease
View SolutionIf the length of a rectangular field is doubled and its breadth is halved (i.e, reduced by 50% ) . What is percentage change in its area ?
View SolutionThe length of a rectangular field is 3 time its breadth . If the area of the field is 147 sq.m, find its length and breadth.
View SolutionThe area of a rectangular fieldis 15 times the sum of its length and breadth. If the length of that field is 40 m, what is the breadth of that field?
View SolutionA rectangular field has its length and breadth in the ratio of 16 : 9. If its perimeter is 750 cm. What is its area?
View Solutionयदि एक आयताकार मैदान की लंबाई 50% बढ़ा दी जाए एवं चौड़ाई 50% घटा दी जाय तो उसके क्षेत्रफल में कितने प्रतिशत की कमी या वृद्धि हो जाएगी?
View SolutionThe length of a rectangular field is 100m. If its perimeter is 300m, what is its breadth?
View SolutionWhat will happen to the area of a rectangle if its (i)Length and breadth are tripled. (ii)Length is doubled and breadth is same. (iii)Length is doubled and breadth is halved.
View Solution
