If a,b,c,d,e,f, g are in contiued proportion, then the value of a.b.c.e.f.g is
d3
d7
d6
None of these
The correct Answer is:C
To solve the problem, we need to understand the concept of continuous proportion. If a,b,c,d,e,f,g are in continuous proportion, it means that the ratios of consecutive terms are equal. This can be expressed mathematically as:
ab=bc=cd=de=ef=fg
From this, we can derive that:
1. a⋅d=b2
2. b⋅e=c2
3. c⋅f=d2
4. d⋅g=e2
Now, we want to find the value of a⋅b⋅c⋅e⋅f⋅g.
1. Express all variables in terms of one variable:
Let's express all variables in terms of a. We can use the relationships derived from the continuous proportion.
- Let b=k⋅a
- Then c=k⋅b=k2⋅a
- Continuing this, we find:
- d=k3⋅a
- e=k4⋅a
- f=k5⋅a
- g=k6⋅a
2. Substitute these expressions into the product:
Now we substitute these expressions into a⋅b⋅c⋅e⋅f⋅g:
a⋅b⋅c⋅e⋅f⋅g=a⋅(k⋅a)⋅(k2⋅a)⋅(k4⋅a)⋅(k5⋅a)⋅(k6⋅a)
3. Combine the terms:
This simplifies to:
=a6⋅k1+2+4+5+6=a6⋅k18
4. Conclusion:
Since k is a constant ratio, the value of a⋅b⋅c⋅e⋅f⋅g is proportional to a6 multiplied by some constant k18.
Thus, the final answer is:
a⋅b⋅c⋅e⋅f⋅g=a6⋅k18
2. b⋅e=c2
3. c⋅f=d2
4. d⋅g=e2
Let's express all variables in terms of a. We can use the relationships derived from the continuous proportion.
- Then c=k⋅b=k2⋅a
- Continuing this, we find:
- d=k3⋅a
- e=k4⋅a
- f=k5⋅a
- g=k6⋅a
Now we substitute these expressions into a⋅b⋅c⋅e⋅f⋅g:
This simplifies to:
Since k is a constant ratio, the value of a⋅b⋅c⋅e⋅f⋅g is proportional to a6 multiplied by some constant k18.
Topper's Solved these Questions
- BOOK - ARIHANT SSCCHAPTER - RATIO, PROPORTION & VARIATIONEXERCISE - EXERCISE (LEVEL 1)61videos
RATIO, PROPORTION & VARIATION
- BOOK - ARIHANT SSCCHAPTER - RATIO, PROPORTION & VARIATIONEXERCISE - EXERCISE (LEVEL 2)49videos
RATIO, PROPORTION & VARIATION
- BOOK - ARIHANT SSCCHAPTER - RATIO, PROPORTION & VARIATIONEXERCISE - INTRODUCTORY EXERCISE - 4.36videos
RATIO, PROPORTION & VARIATION
- BOOK - ARIHANT SSCCHAPTER - RATIO AND PROPORTIONEXERCISE - HIGHER SKILL LEVEL QUESTIONS21videos
RATIO AND PROPORTION
- BOOK - ARIHANT SSCCHAPTER - SEQUENCE, SERIES & PROGRESSIONSEXERCISE - Final Round18videos
SEQUENCE, SERIES & PROGRESSIONS
Similar Questions
If (a,b),(c,d),(e,f) are the vertices of a triangle such that a, c, e are in G. P. with common ratio r and b, d, f are in G. P. with common ratio s, then the area of the triangle is
View SolutionArea of the triangle with vertces (a,b),(x1,y1) and (x2,y2) where a,x1,x2 are in G.P with common ratio r and b,y1,y2 are in G.P with common ratio s is
View Solution
Knowledge Check
- Question 1 - Select One
If a,b,c are in H.P, b,c,d are in G.P and c,d,e are in A.P. , then the value of e is
Aab2(2a−b)2Ba2b(2a−b)2Ca2b2(2a−b)2DNone of these - Question 2 - Select One
If a,b,c,d,e,f are in AP, then the value of e-c will be
A2(c−a)B2(f−d)C2(d−c)Dd-c - Question 3 - Select One
If a, b, c, d, e, f are A.M's between 2 and 12, then a + b + c + d + e + f is equal to
A14B42C84Dnone of these
If a, b, c, d, e, f are A.M's between 2 and 12, then a + b + c + d + e + f is equal to
View Solutiona.
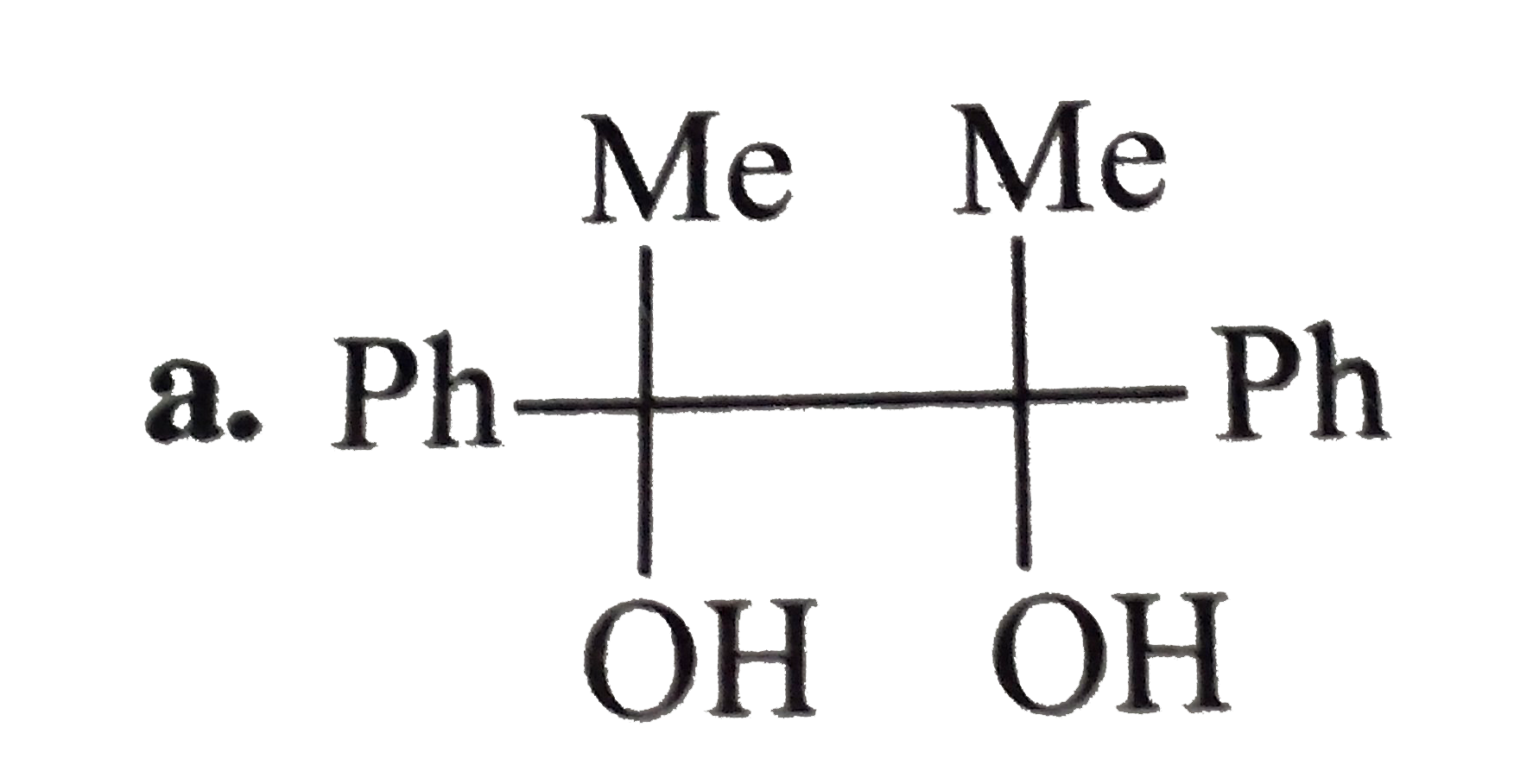 b.
b. 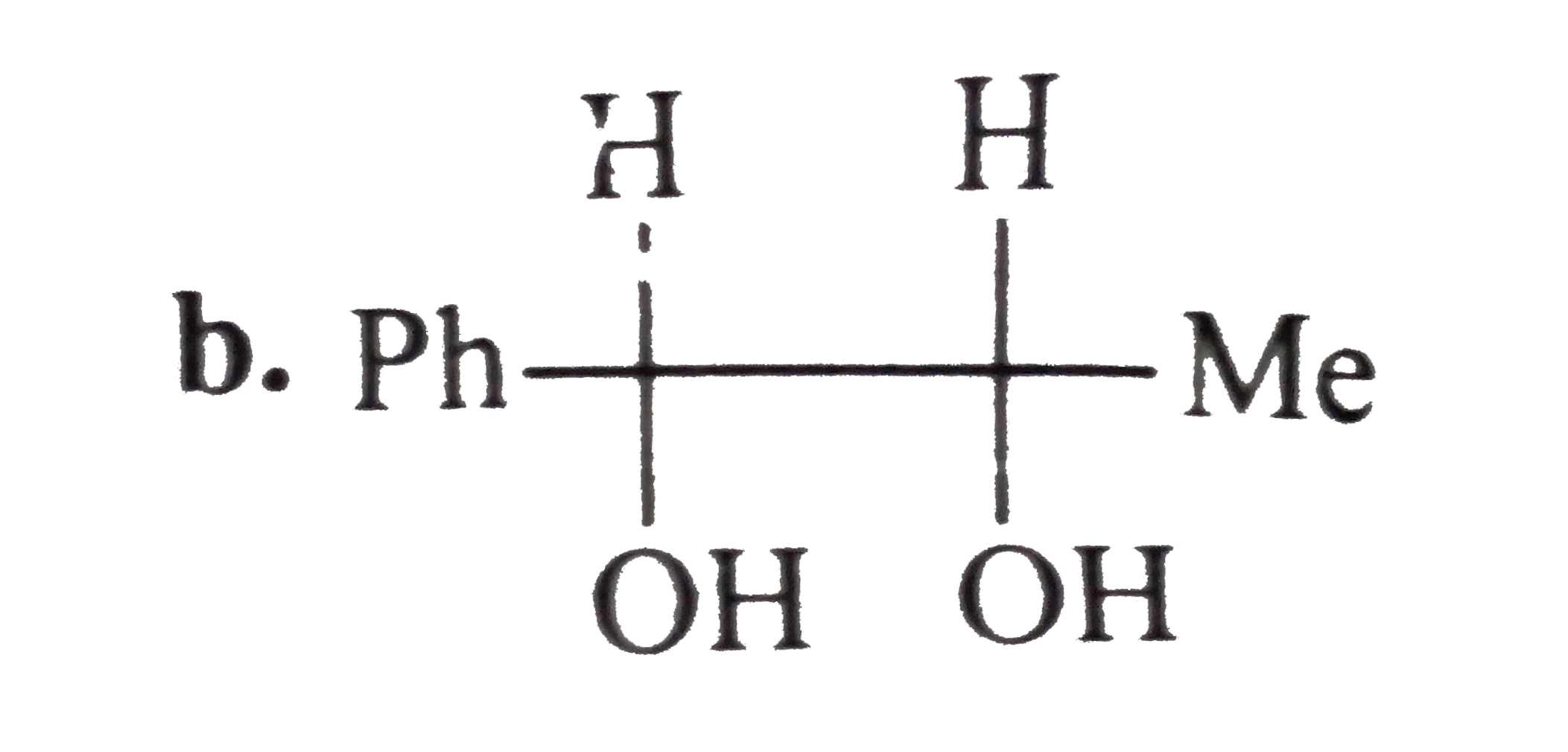
c.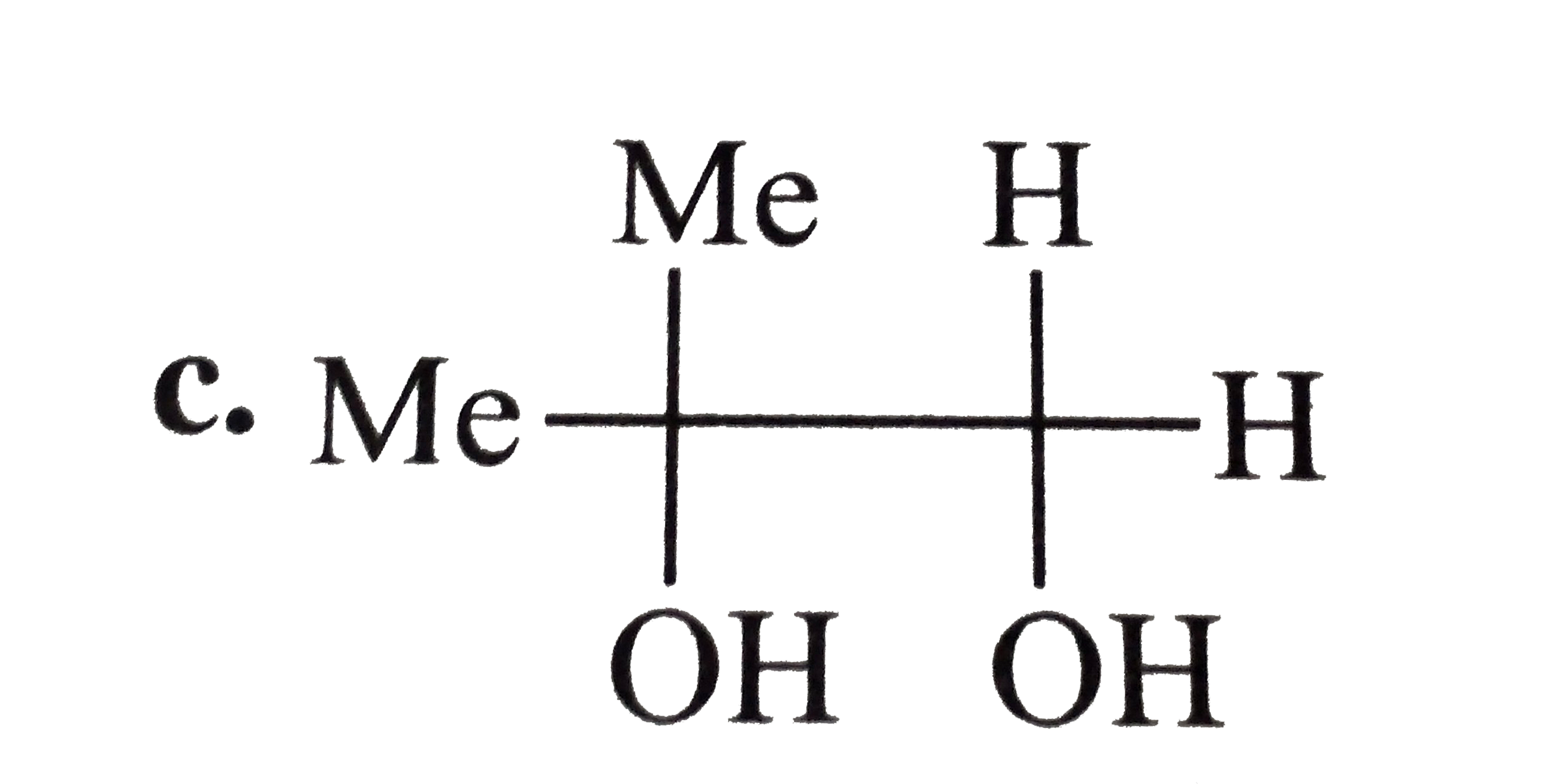 d.
d. 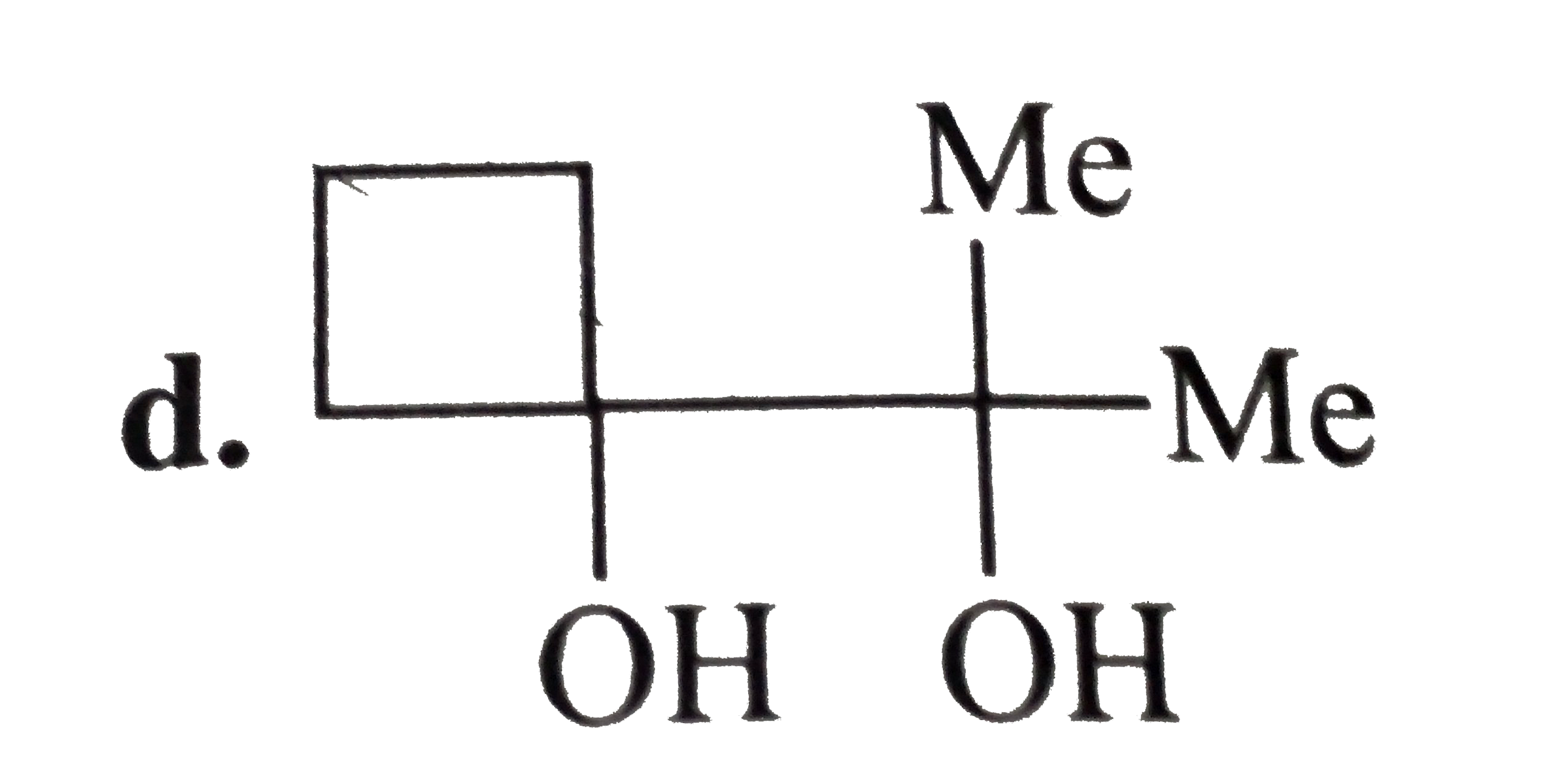
e.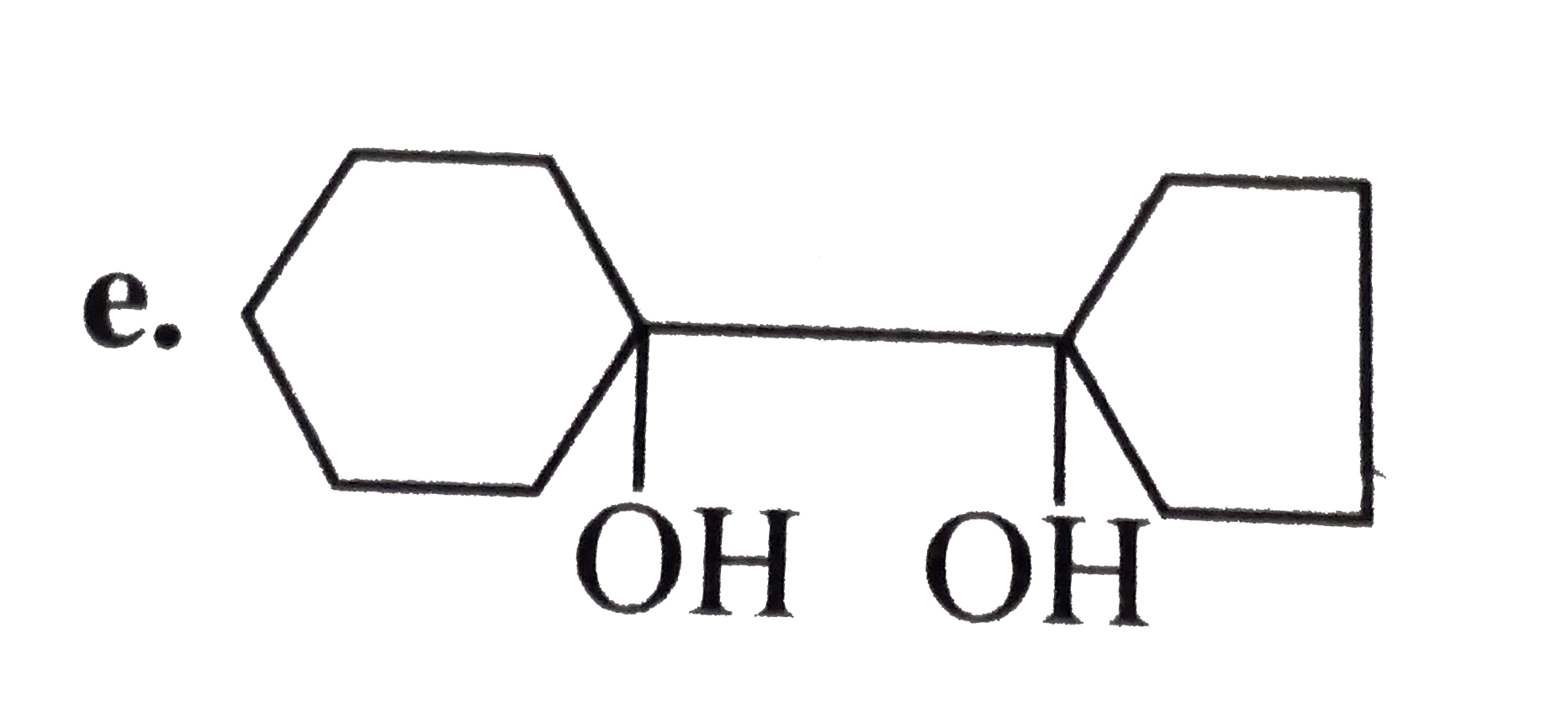 f.
f. 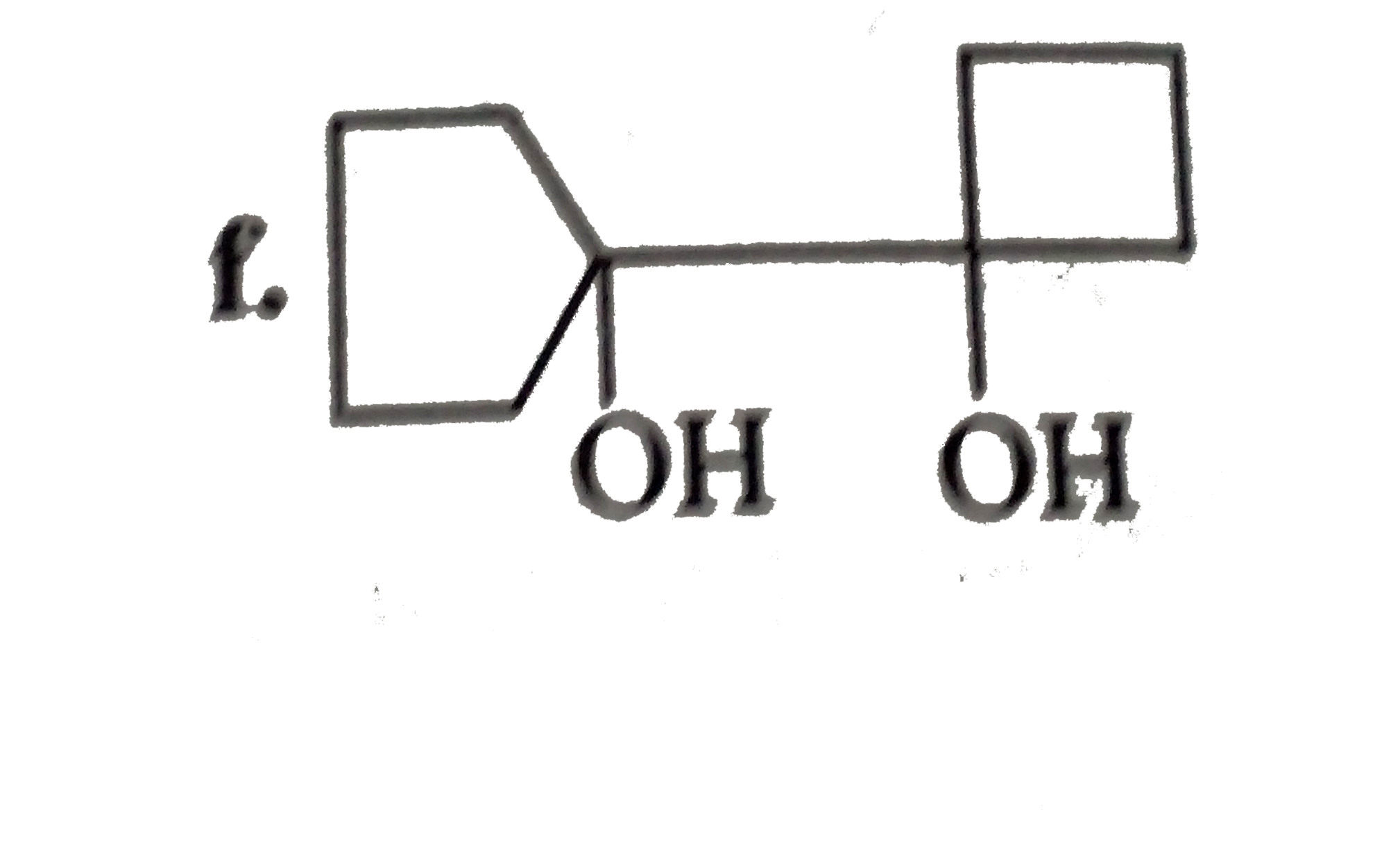
g.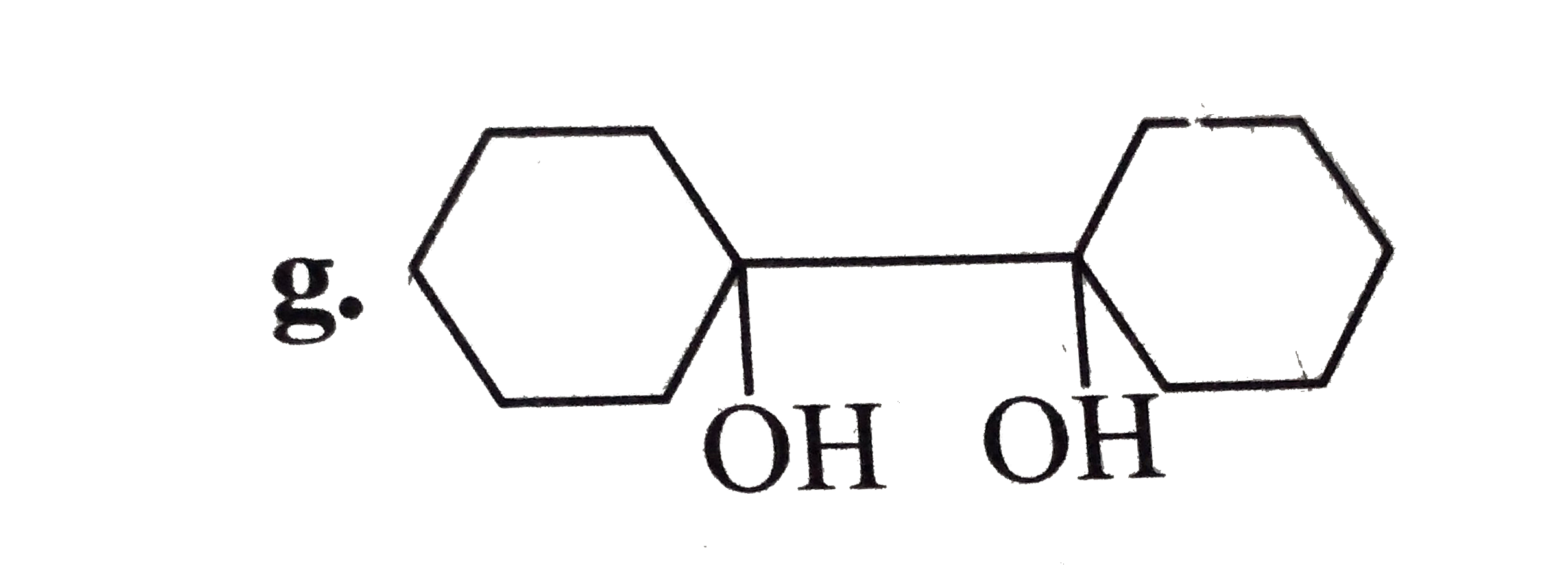 h.
h. 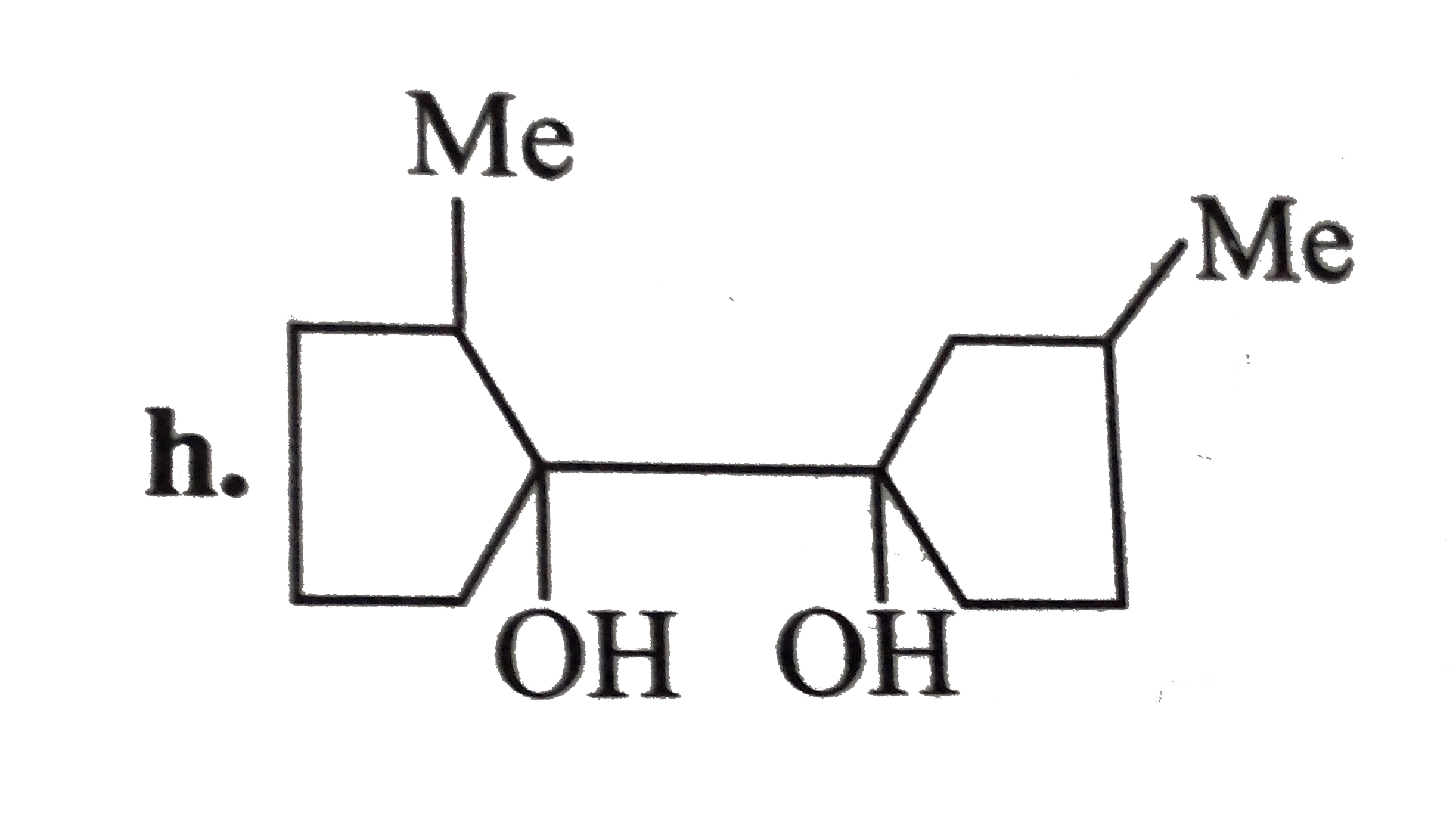 View Solution
View SolutionIf U = {a,b,c,d,e,f,g,h} , find the complement of the following sets:
A= {a,b,c} , B ={d,e,f,g} , C ={a,c,eg}, D = {f,g,h,a}.View SolutionDistinguish between the following:
a.
b.
c.
d.
e.
f.
g. View Solution
View SolutionLet f, g and h be real-valued functions defined on the interval [0, 1] by f(x)=ex^2+e−x^2, g(x)=xex^2+e−x^2 and h(x)=x2ex^2+e−x^2 . If a,b, and c denote respectively, the absolute maximum of f, g and h on [0, 1], then a=b and c≠b (b) a=c and a≠b a≠b and c≠b (d) a=b=c
View Solution
